Câu hỏi
Hợp lực F của hai lực F1 và lực F2 có độ lớn \(8\sqrt 2 N\); lực F tạo với hướng của lực F1 góc 45° và F1 = 8 N. Xác định hướng và độ lớn của lực F2.
- A vuông góc với lực F1 và F2 = 8 N
- B vuông góc với lực F1 và F2 = 6 N
- C cùng phương ngược chiều với F1 và F2 = 8 N
- D cùng phương ngược chiều với F1 và F2 = 6 N
Phương pháp giải:
Sử dụng các công thức hình học
Lời giải chi tiết:
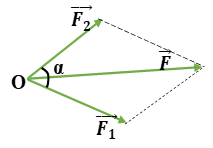
Ta có: \(\left\{ \begin{array}{l}F = 8\sqrt 2 N\\{F_1} = 8N\\\left( {\overrightarrow F ;\overrightarrow {{F_1}} } \right) = {45^0}\end{array} \right. \Rightarrow {F_1}\; = F.cos{45^0} \Rightarrow \overrightarrow {{F_2}} \bot \overrightarrow {{F_1}} \)
→ Độ lớn của F2 là: \({F_2}\; = F.sin{45^0} = 8\sqrt 2 .\sin {45^0} = 8N\)
Chọn A
Câu hỏi trước
