Phương pháp giải:

- Phân tích các lực tác dụng vào vật

- Điều kiện cân bằng của một chất điểm là hợp lực của các lực tác dụng lên nó phải bằng không:

\(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + ... = \overrightarrow 0 \)

Lời giải chi tiết:

Các lực tác dụng vào O gồm:

+ Lực kéo của vật nặng: \(\overrightarrow P \) (P = 20N)

+ Lực căng của dây OA: \(\overrightarrow {{T_A}} \)

+ Lực căng của dây OB: \(\overrightarrow {{T_B}} \)

Biểu diễn các lực tác dụng vào vật:

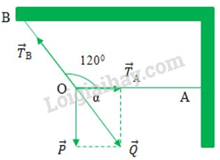
Chất điểm O nằm cân bằng: \(\overrightarrow {{T_A}}  + \overrightarrow {{T_B}}  + \overrightarrow P  = 0 \Leftrightarrow \left( {\overrightarrow {{T_A}}  + \overrightarrow P } \right) + \overrightarrow {{T_B}}  = 0 \Leftrightarrow \overrightarrow Q  + \overrightarrow {{T_B}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow Q  \uparrow  \downarrow \overrightarrow {{T_B}} \\Q = {T_B}\end{array} \right.\)

\( \Rightarrow \alpha  = \left( {\overrightarrow {{T_A}} ;\overrightarrow Q } \right) = 180 - 120 = {60^0}\)

Có \(\overrightarrow {{T_A}}  \bot \overrightarrow P  \Rightarrow \)Hình bình hành là hình chữ nhật

Xét tam giác vuông OT_AQ có: \(\left\{ \begin{array}{l}{T_A} = \dfrac{P}{{\tan \alpha }} = \dfrac{{20}}{{\tan 60}} = \dfrac{{20}}{{\sqrt 3 }}N\\Q = \dfrac{P}{{\sin \alpha }} = \dfrac{{20}}{{\sin 60}} = \dfrac{{40}}{{\sqrt 3 }}N\end{array} \right.\)

Lại có: \(Q = {T_B} = \dfrac{{40}}{{\sqrt 3 }}N\)

Chọn C