Phương pháp giải:

Vật (1) : Vật chuyển động

Vật (2): Hệ quy chiếu chuyển động

Vật (3): Hệ quy chiếu đứng yên.

Ta có:

 + \(\overrightarrow {{v_{12}}} \): vận tốc của vật chuyển động (1) so với hệ quy chiếu chuyển động (2) → Vận tốc tương đối

 + \(\overrightarrow {{v_{13}}} \): vận tốc của vật chuyển động (1) so với hệ quy chiếu đứng yên (3) → Vận tốc tuyệt đối

 + \(\overrightarrow {{v_{23}}} \): vận tốc của hệ quy chiếu chuyển động (2) so với hệ quy chiếu chuyển động (3) → Vận tốc kéo theo.

Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Lời giải chi tiết:

Vật (1): Thuyền

Vật (2): Dòng nước

Vật (3): Bờ sông

Ta có: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Người chèo thuyền qua sông với vận tốc 5,4km/h là: \({v_{12}} = 9km/h = 2,5m/s\)

(Vận tốc của thuyền khi nước đứng yên)

Có \(\overrightarrow {{v_{12}}}  \bot \overrightarrow {{v_{23}}} \)

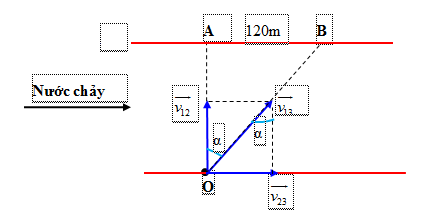
Ta có: \(\left\{ \begin{array}{l}OA = 600m{\rm{ }}\\AB = 120m\end{array} \right. \Rightarrow \tan \alpha  = \dfrac{{AB}}{{OA}} = \dfrac{{120}}{{600}} = \dfrac{1}{5}\)

Mặt khác: \(\tan \alpha  = \dfrac{{{v_{23}}}}{{{v_{12}}}} \Rightarrow {v_{23}} = {v_{12}}.\tan \alpha  = 2,5.\dfrac{1}{5} = 0,5m/s\)

Chọn B