Câu hỏi
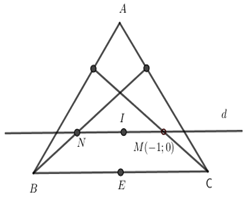
Cho tam giác ABC cân tại \(A,\) đường thẳng \(BC\) có phương trình \(x + 2y - 2 = 0\). Đường cao kẻ từ \(B\) có phương trình \(x - y + 4 = 0,\)điểm \(M\left( { - 1;0} \right)\) thuộc đường cao kẻ từ \(C.\) Xác định toạ độ ba điểm \(A,\, B,\, C.\)
- A \(A\left( { - \frac{{13}}{{10}}; - \frac{{19}}{{10}}} \right);B\left( { - 2;2} \right);C\left( { - \frac{4}{5};\frac{7}{5}} \right)\)
- B \(A\left( {\frac{{13}}{{10}}; - \frac{{19}}{{10}}} \right);B\left( { - 2;2} \right);C\left( { - \frac{4}{5}; - \frac{7}{5}} \right)\)
- C \(A\left( {\frac{{13}}{{10}};\frac{{19}}{{10}}} \right);B\left( { - 2;2} \right);C\left( { - \frac{4}{5};\frac{7}{5}} \right)\)
- D \(A\left( { - \frac{{13}}{{10}}; - \frac{{19}}{{10}}} \right);B\left( { - 2;2} \right);C\left( {\frac{4}{5};\frac{7}{5}} \right)\)
Phương pháp giải:
\(\Delta ABC\) cân tại \(A \Rightarrow AB = AC.\)
Lời giải chi tiết:
Toạ độ điểm \(B\) là nghiệm của hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + 2y - 2 = 0}\\{x - y + 4 = 0}\end{array} \Rightarrow B\left( { - 2;\,\,2} \right)} \right.\)
Gọi \(d\) là đường thẳng qua \(M\) và song song với \(BC\)
\( \Rightarrow d:x + 1 + 2y = 0 \Leftrightarrow x + 2y + 1 = 0.\)
Gọi \(N\) là giao điểm của \(d\) với đường cao kẻ từ \(B\)
\( \Rightarrow \) Toạ độ của \(N\) là nghiệm của hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x - y + 4 = 0}\\{x + 2y + 1 = 0}\end{array} \Rightarrow N\left( { - 3;1} \right)} \right.\)
Gọi \(I\) là trung điểm của \(MN \Rightarrow I\left( { - 2;\,\,\frac{1}{2}} \right).\)
Gọi \(E\) là trung điểm của \(BC \Rightarrow IE\) là đường trung trực của \(BC \Rightarrow IE:4x - 2y + 9 = 0\)
Toạ độ \(E\) là nghiệm của hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + 2y - 2 = 0}\\{4x - 2y + 9 = 0}\end{array} \Rightarrow E\left( {\frac{{ - 7}}{5};\frac{{17}}{{10}}} \right) \Rightarrow C\left( {\frac{{ - 4}}{5};\frac{7}{5}} \right)} \right.\)
Đường thẳng \(CA\) qua \(C\) và vuông góc với \(BN\)
\( \Rightarrow CA:\,\,x + \frac{4}{5} + y - \frac{7}{5} = 0 \Leftrightarrow x + y - \frac{3}{5} = 0.\)
Toạ độ đỉnh \(A\) là nghiệm của hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{4x - 2y + 9 = 0}\\{x + y - \frac{3}{5} = 0}\end{array} \Rightarrow } \right.A\left( { - \frac{{13}}{{10}};\frac{{19}}{{10}}} \right)\)
Chọn A