Lời giải chi tiết:

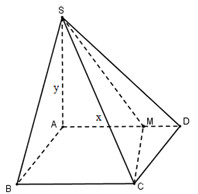
\(\begin{array}{l}{S_{ABCM}} = {S_{ABCD}} - {S_{CMD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {a^2} - \dfrac{1}{2}a\left( {a - x} \right) = \dfrac{{{a^2}}}{2} + \dfrac{{ax}}{2}\end{array}\)

\(\begin{array}{l} \Rightarrow {V_{S.ABCM}} = \dfrac{1}{3}y\left( {\dfrac{{{a^2}}}{2} + \dfrac{{ax}}{2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{6}a\sqrt {{a^2} - {x^2}} \left( {a + x} \right)\,\,\left( {y = \sqrt {{a^2} - {x^2}} } \right)\end{array}\)

Đặt \(f\left( x \right) = \dfrac{1}{6}a\sqrt {{a^2} - {x^2}} \left( {a + x} \right)\,;\,\,\,x \in \left( {0;a} \right)\)

\(\begin{array}{l}f'(x) = \dfrac{1}{6}.a.\left[ {\dfrac{{ - x\left( {a + x} \right)}}{{\sqrt {{a^2} - {x^2}} }} + \sqrt {{a^2} - {x^2}} } \right]\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{6}.a\left[ {\dfrac{{ - x\left( {a + x} \right) + {a^2} - {x^2}}}{{\sqrt {{a^2} - {x^2}} }}} \right]\\\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{6}.a\dfrac{{ - 2{x^2} - ax + {a^2}}}{{\sqrt {{a^2} - {x^2}} }}\\f'(x) = 0 \Rightarrow  - 2{x^2} - ax + {a^2} = 0 \Rightarrow \left[ \begin{array}{l}x =  - a\\x = \dfrac{a}{2}\end{array} \right.\end{array}\)

Lập bảng biến thiên ta được:

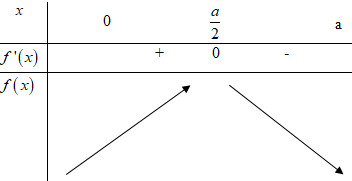
\(\begin{array}{l}{V_{max}} \Leftrightarrow x = \dfrac{a}{2}\\ \Rightarrow {V_{max}} = \dfrac{1}{6}a.\sqrt {{a^2} - \dfrac{{{a^2}}}{4}} \left( {a + \dfrac{a}{2}} \right) = \dfrac{1}{6}a\dfrac{{a\sqrt 3 }}{2}.\dfrac{{3a}}{2} = \dfrac{{{a^3}\sqrt 3 }}{8}\end{array}\)

Chọn D