Lời giải chi tiết:

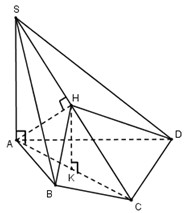
Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow AC\)là hình chiếu của SC trên (ABCD)\( \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = {60^0}\)

\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại A

Xét tam giác vuông SAC có:

\(SA = AC.\tan 60 = a\sqrt 2 .\sqrt 3  = a\sqrt 6 ;\) \(SC = \dfrac{{AC}}{{{\rm{cos60}}}} = \dfrac{{a\sqrt 2 }}{{\dfrac{1}{2}}} = 2a\sqrt 2 \)   

Áp dụng hệ thức lượng trong tam giác vuông SAC có: \(A{C^2} = HC.SC \Rightarrow \dfrac{{HC}}{{SC}} = \dfrac{{A{C^2}}}{{S{C^2}}} = \dfrac{{2{a^2}}}{{8{a^2}}} = \dfrac{1}{4}\)

Trong (SAC) kẻ \(HK//SA \Rightarrow HK \bot \left( {ABCD} \right)\)

Ta có: \(\dfrac{{HK}}{{SA}} = \dfrac{{HC}}{{SC}} = \dfrac{1}{4} \Rightarrow HK = \dfrac{1}{4}SA = \dfrac{{a\sqrt 6 }}{4}\)

Vậy \({V_{H.ABCD}} = \dfrac{1}{3}HK.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{4}.\dfrac{{3{a^2}}}{2} = \dfrac{{{a^3}\sqrt 6 }}{8}\)  

Chọn D.