Lời giải chi tiết:

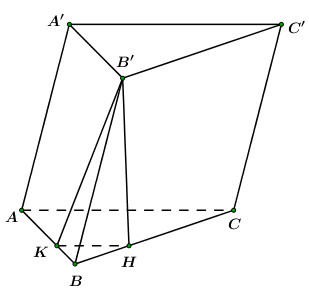
Ta có \(\Delta ABC\) vuông tại \(A,\)  có \(BC = 2a\) và \(\angle ABC = {60^0}\)

\( \Rightarrow \left\{ \begin{array}{l}AB = a\\AC = a\sqrt 3 \end{array} \right.\) \( \Rightarrow {S_{ABC}} = \frac{1}{2}AB.AC = \frac{{{a^2}\sqrt 3 }}{2}.\)

Gọi \(H\) là hình chiếu vuông góc của \(B'\) lên \(BC\)

\( \Rightarrow H \in BC\,\,\) (do \(\angle B'BC\) là góc nhọn).

Lại có: \(\left( {BCC'B'} \right) \bot \left( {ABC} \right)\) \( \Rightarrow BH \bot \left( {ABC} \right)\)

Kẻ \(HK//AC\,\,\left( {K \in AB} \right)\) \( \Rightarrow HK \bot AB\)

\(\begin{array}{l} \Rightarrow \angle \left( {\left( {ABB'A'} \right),\,\,\left( {ABC} \right)} \right) = \angle B'KH = {45^0}\\ \Rightarrow B'H = KH\,\,\,\,\,\left( 1 \right)\end{array}\)

Ta có: \(\Delta BB'H\) vuông tại \(H \Rightarrow BH = \sqrt {4{a^2} - B'{H^2}} \,\,\,\,\,\,\,\,\left( 2 \right)\)

Mặt khác, \(HK//AC\) \( \Rightarrow \frac{{BH}}{{BC}} = \frac{{HK}}{{AC}}kBH = \frac{{HK.2a}}{{a\sqrt 3 }}\,\,\,\,\left( 3 \right)\)

Từ (1), (2) và (3) ta có: \(\sqrt {4{a^2} - B'{H^2}}  = \frac{{B'H.2a}}{{a\sqrt 3 }} \Rightarrow B'H = a\sqrt {\frac{{12}}{7}} .\)

\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{ABC}}.B'H = \frac{{{a^2}\sqrt 3 }}{2}.a\sqrt {\frac{{12}}{7}}  = \frac{{3{a^3}}}{{\sqrt 7 }}.\)

Chọn B.