Phương pháp giải:

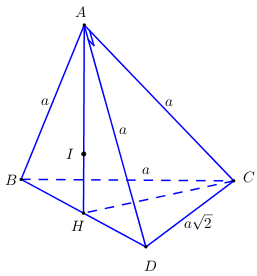
Xét tam giác vuông \(ACD\) có: \(AD = \sqrt {C{D^2} - A{C^2}}  = \sqrt {2{a^2} - {a^2}}  = a\) \( \Rightarrow \Delta ABD\) cân tại \(A\).

Gọi \(H\) là trung điểm của \(BD \Rightarrow AH \bot BD\).

Ta có \(\left\{ \begin{array}{l}\left( {BCD} \right) \bot \left( {ABD} \right)\,\,\left( {gt} \right)\\\left( {BCD} \right) \cap \left( {ABD} \right) = BD\\\left( {ABD} \right) \supset AH \bot BD\end{array} \right. \Rightarrow AH \bot \left( {BCD} \right)\).

Tứ diện \(ABCD\) có \(AB = AC = AD = a \Rightarrow H\) là tâm đường tròn ngoại tiếp tam giác \(BCD\).

Mà \(H\) là trung điểm của \(BD \Rightarrow \Delta BCD\) vuông tại \(C \Rightarrow \) \(BD = \sqrt {B{C^2} + C{D^2}}  = a\sqrt 3 \) và \(AH\) là trục của \(\left( {BCD} \right)\).

Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABD \Rightarrow IA = IB = ID\) và \(I \in AH\).

\(I \in AH \Rightarrow IB = IC = ID \Rightarrow IA = IB = IC = ID \Rightarrow I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\).

Xét tam giác vuông \(ABH:\,\,AH = \sqrt {A{B^2} - B{H^2}}  = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}}  = \dfrac{a}{2}\).

\( \Rightarrow {S_{ABD}} = \dfrac{1}{2}AH.BD = \dfrac{1}{2}.\dfrac{a}{2}.a\sqrt 3  = \dfrac{{{a^2}\sqrt 3 }}{4}\)\( \Rightarrow IA = R = \dfrac{{AB.AD.BD}}{{4{S_{\Delta ABD}}}} = \dfrac{{a.a.a\sqrt 3 }}{{4.\dfrac{{{a^2}\sqrt 3 }}{4}}} = a\).

Vậy \({V_{cau}} = \dfrac{{4\pi {a^3}}}{3}\).

Chọn A