Câu hỏi
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây:
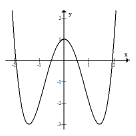
- A \(y = {x^4} - {x^2} + 1\)
- B \(y = {x^4} - 4{x^2} + 1\)
- C \(y = - {x^4} + 4{x^2} + 1\)
- D \(y = {x^4} - 4{x^2} - 1\)
Phương pháp giải:
+) Tính \(\mathop {\lim }\limits_{x \to + \infty } y\), suy ra dấu của hệ số \(a\).
+) Dựa vào các điểm đồ thị hàm số đi qua.
+) Dựa vào các điểm cực trị của hàm số.
Lời giải chi tiết:
+) Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \Rightarrow a > 0 \Rightarrow \) Loại đáp án C.
+) Đồ thị hàm số đi qua \(\left( {0;1} \right) \Rightarrow \) Loại đáp án D.
+) Xét đáp án A ta có \(y' = 4{x^3} - 2x = 0 \Leftrightarrow 2x\left( {2{x^2} - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{1}{{\sqrt 2 }} < 1\\x = - \dfrac{1}{{\sqrt 2 }} > - 1\end{array} \right.\). Do đó loại đáp án A.
Chọn B







