Phương pháp giải:

Sử dụng \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) \Rightarrow F'\left( x \right) = f\left( x \right)\)

Từ đó ta lập bảng xét dấu của hàm \(F'\left( x \right)\) để tìm số cực trị của hàm số \(F\left( x \right)\)

Lời giải chi tiết:

Vì hàm số \(f\left( x \right) = {x^2}\left( {x - 1} \right){e^{3x}}\) có một nguyên hàm là hàm số \(F\left( x \right)\) nên \(F'\left( x \right) = f\left( x \right) = {x^2}\left( {x - 1} \right){e^{3x}}\)

Xét \(F'\left( x \right) = 0 \Leftrightarrow {x^2}\left( {x - 1} \right){e^{3x}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)

Bảng biến thiên của hàm \(F'\left( x \right).\)

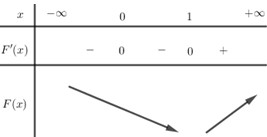
Vậy hàm số có 1 điểm cực trị.

Chọn A.