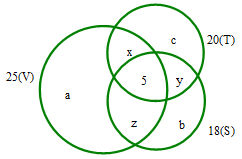Phương pháp giải:

Gọi \(a,b,c\) theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;

\(x\) là số học sịnh chỉ thích hai môn là văn và toán

\(y\) là số học sịnh chỉ thích hai môn là Sử và toán

\(z\) là số học sịnh chỉ thích hai môn là văn và Sử

Lập hệ phương trình giải tìm \(a + b + c\)

Lời giải chi tiết:

Gọi \(a,b,c\) theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;

\(x\) là số học sịnh chỉ thích hai môn là văn và toán

\(y\) là số học sịnh chỉ thích hai môn là Sử và toán

\(z\) là số học sịnh chỉ thích hai môn là văn và Sử

Ta có số em thích ít nhất một môn là \(45 - 6 = 39\)

Sựa vào biểu đồ ven ta có hệ phương trình

\(\left\{ \begin{array}{l}a + x + z + 5 = 25\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\b + y + z + 5 = 18\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\\c + x + y + 5 = 20\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)\\x + y + z + a + b + c + 5 = 39\,\,\,\,(4)\end{array} \right.\)

Cộng vế với vế (1), (2), (3) ta có

\(a + b + c + 2\left( {x + y + z} \right) + 15 = 63\) (5)

Từ (4) và (5) ta có

\(\begin{array}{l}a + b + c + 2\left( {39 - 5 - a - b - c} \right) + 15 = 63\\ \Leftrightarrow a + b + c = 20.\end{array}\)

Vậy chỉ có \(20\) em thích chỉ một môn trong ba môn trên.

Chọn  B.