Câu hỏi
Cho hàm số \(f\left( x \right) = m{x^4} + n{x^3} + p{x^2} + qx + 2019\) (với \(m,n,p,q \in \mathbb{R}\)). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên dưới. Tập nghiệm \(S\) của phương trình \(f\left( x \right) = 2019\) có số phần tử là
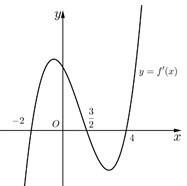
- A \(1\).
- B \(2\).
- C \(3\).
- D \(4\).
Lời giải chi tiết:
Chọn D.
Câu hỏi trước
