Câu hỏi
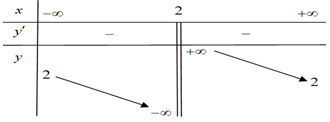
Hàm số nào sau đây có bảng biến thiên như hình vẽ bên?.
- A \(y = \frac{{x + 3}}{{x - 2}}.\)
- B \(y = \frac{{2x - 1}}{{x - 2}}.\)
- C \(y = \frac{{2x - 3}}{{x + 2}}.\)
- D \(y = \frac{{2x - 5}}{{x - 2}}.\)
Phương pháp giải:
- Tìm TCĐ, TCN của đồ thị hàm số.
- Đối chiếu các đáp án và kết luận.
Lời giải chi tiết:
Quan sát bảng biến thiên ta thấy:
Đồ thị hàm số đã cho có đường TCĐ là \(x = 2\) và đường TCN là \(y = 2\), hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
+) Đáp án A: đồ thị hàm số \(y = \frac{{x + 3}}{{x - 2}}\) có đường TCĐ \(x = 2\) và TCN \(y = 1\) (loại A).
+) Đáp án B: đồ thị hàm số \(y = \frac{{2x - 1}}{{x - 2}}\) có đường TCĐ \(x = 2\) và TCN \(y = 2\).
Hàm số có \(y' = \frac{{ - 3}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x \ne 2\) nên nghịch biến trên mỗi khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
Chọn B.