Phương pháp giải:

+) Áp dụng định lí Cosin trong tam giác tính HC.

+) Áp dụng định lí Pytago đảo chứng minh $HA \bot CA$

+) Chứng minh $\widehat {\left( {\left( {ABC} \right);\left( {ACC'A'} \right)} \right)} = \widehat {\left( {AH;AC'} \right)}$

+) Sử dụng định lí Pytago tính C’H. Chứng minh tam giác C’AH vuông cân.

Lời giải chi tiết:

Gọi H là trung điểm của BC. Theo giả thiết ta có: $C'H \bot \left( {ABC} \right)$

Xét tam giác ABC có:

$\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.cos\widehat {BAC} = 4{a^2} + {a^2} - 2.2a.a.\left( { - \dfrac{1}{2}} \right) = 7{a^2} \Rightarrow BC = a\sqrt 7  \Rightarrow HC = \dfrac{{a\sqrt 7 }}{2}\\cos\widehat {ACB} = \dfrac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}} = \dfrac{{{a^2} + 7{a^2} - 4{a^2}}}{{2.a.a\sqrt 7 }} = \dfrac{2}{{\sqrt 7 }}\\ \Rightarrow A{H^2} = A{C^2} + H{C^2} - 2AC.HC.cos\widehat {ACH} = {a^2} + \dfrac{7}{4}{a^2} - 2.a.\dfrac{{a\sqrt 7 }}{2}.\dfrac{2}{{\sqrt 7 }} = \dfrac{{3{a^2}}}{4} \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}\end{array}$

Ta có: $A{H^2} + A{C^2} = \dfrac{{3{a^2}}}{4} + {a^2} = \dfrac{{7{a^2}}}{4} = H{C^2}$

$\Delta ACH$vuông tại A (Định lý Pi – ta – go đảo) $\Rightarrow HA \bot CA$

Vì $C'H \bot \left( {ABC} \right) \Rightarrow C'H \bot AC$

$\Rightarrow AC \bot \left( {AHC'} \right) \Rightarrow AC \bot AC'$

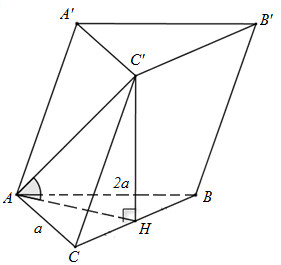
Ta có:

$\left. \begin{array}{l}\left( {ABC} \right) \cap \left( {ACC'A'} \right) = AC\\AH \bot AC\\AC' \bot AC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {ABC} \right);\left( {ACC'A'} \right)} \right)} = \widehat {\left( {AH;AC'} \right)} = \widehat {C'AH}$

(Vì $C'H \bot \left( {ABC} \right) \Rightarrow C'H \bot AH \Rightarrow \Delta C'HA$ vuông tại H $\Rightarrow \widehat {C'AH} < {90^0}$)

$C'H \bot \left( {ABC} \right) \Rightarrow C'H \bot BC$

Xét tam giác vuông $CC'H$có: $C'H = \sqrt {CC{'^2} - H{C^2}}  = \sqrt {\dfrac{{10{a^2}}}{4} - \dfrac{{7{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}$

$\Rightarrow C'H = AH \Rightarrow \Delta C'AH$ vuông cân tại H $\Rightarrow \widehat {C'AH} = {45^0}$

Chọn C.