Phương pháp giải:

Sử dụng công thức tính tỉ số thể tích.

Lời giải chi tiết:

Ta có: \(\left\{ \begin{array}{l}\left( {MNB'A'} \right) \cap \left( {ACC'A'} \right) = A'M\\\left( {MNB'A'} \right) \cap \left( {BCC'B'} \right) = B'N\\\left( {ACC'A'} \right) \cap \left( {BCC'B'} \right) = CC'\end{array} \right. \Rightarrow A'M,\,\,B'N,\,\,CC'\) đồng quy tại \(S\).

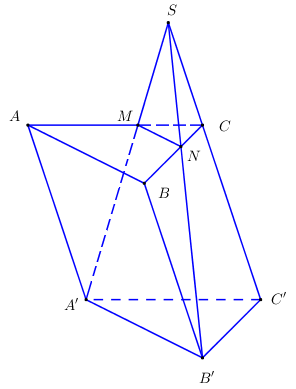
Áp dụng định lí Ta-let ta có:

\(\dfrac{{SM}}{{SA'}} = \dfrac{{MN}}{{A'B'}} = \dfrac{{MN}}{{AB}} = \dfrac{{CM}}{{CA}} = k = \dfrac{{SN}}{{SB'}} = \dfrac{{SC}}{{SC'}}\)

\(\begin{array}{l} \Rightarrow \dfrac{{{V_{S.MNC}}}}{{{V_{S.A'B'C'}}}} = \dfrac{{SM}}{{SA'}}.\dfrac{{SN}}{{SB'}}.\dfrac{{SC}}{{SC'}} = {k^3}\\ \Rightarrow \dfrac{{{V_1}}}{{{V_{S.A'B'C'}}}} = 1 - {k^3} \Rightarrow {V_1} = \left( {1 - {k^3}} \right){V_{S.A'B'C'}}.\end{array}\)

Ta có : \(\dfrac{{SC}}{{SC'}} = k \Rightarrow \dfrac{{SC' - CC'}}{{SC'}} = k \Leftrightarrow \dfrac{{CC'}}{{SC'}} = 1 - k\)

\(\begin{array}{l} \Rightarrow \dfrac{{{V_{S.A'B'C'}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}SC'}}{{CC'}} = \dfrac{1}{{3\left( {1 - k} \right)}} \Rightarrow {V_{S.A'B'C'}} = \dfrac{{{V_{ABC.A'B'C'}}}}{{3\left( {1 - k} \right)}}\\ \Rightarrow {V_1} = \left( {1 - {k^3}} \right){V_{S.A'B'C'}} = \left( {1 - {k^3}} \right)\dfrac{{{V_{ABC.A'B'C'}}}}{{3\left( {1 - k} \right)}} = \dfrac{{1 + k + {k^2}}}{3}{V_{ABC.A'B'C'}}\end{array}\)

Ta có: \(\dfrac{{{V_1}}}{{{V_2}}} = 2 \Leftrightarrow {V_1} = \dfrac{2}{3}{V_{ABC.A'B'C'}}\)\( \Rightarrow \dfrac{{1 + k + {k^2}}}{3} = \dfrac{2}{3} \Leftrightarrow 1 + k + {k^2} = 2 \Leftrightarrow k = \dfrac{{\sqrt 5  - 1}}{2}\).

Chọn A