Phương pháp giải:

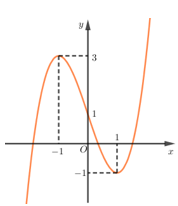
- Vẽ đồ thị hàm số \(y = f\left( x \right) = {x^3} - 3x + 1\) trên hệ trục tọa độ.

- Sử dụng mối tương giao đồ thị nhận xét số giao điểm của đường thẳng với đồ thị hàm số, từ đó suy ra số nghiệm.

Lời giải chi tiết:

Hàm số \(y = f\left( x \right) = {x^3} - 3x + 1\) xác định trên \(\mathbb{R}\) và có \(f'\left( x \right) = 3{x^2} - 3 = 0 \Leftrightarrow x =  \pm 1\).

Đồ thị :

Sử dụng MTCT ta có \(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_1} \in \left( { - 2; - 1} \right)\\x = {x_2} \in \left( {0;1} \right)\\x = {x_3} \in \left( {1;2} \right)\end{array} \right.\)

\( \Rightarrow f\left( {f\left( x \right)} \right) = 0 \Leftrightarrow f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = {x_1} \in \left( { - 2; - 1} \right)\,\,\left( 1 \right)\\f\left( x \right) = {x_2} \in \left( {0;1} \right)\,\,\left( 2 \right)\\f\left( x \right) = {x_3} \in \left( {1;2} \right)\,\,\left( 3 \right)\end{array} \right.\)

+) Đường thẳng \(y = {x_1} \in \left( { - 2; - 1} \right)\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại duy nhất \(1\) điểm nên \(\left( 1 \right)\) có \(1\) nghiệm duy nhất.

+) Đường thẳng \(y = {x_2} \in \left( {0;1} \right)\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại \(3\) điểm nên \(\left( 2 \right)\) có \(3\) nghiệm phân biệt. Hơn nữa trong ba nghiệm này không có nghiệm nào trùng với nghiệm của \(\left( 1 \right)\).

+) Đường thẳng \(y = {x_2} \in \left( {1;2} \right)\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại \(3\) điểm nên \(\left( 3 \right)\) có \(3\) nghiệm phân biệt. Hơn nữa trong ba nghiệm này không có nghiệm nào trùng với nghiệm của \(\left( 1 \right)\) và \(\left( 2 \right)\).

Vậy tổng số nghiệm của ba phương trình \(\left( 1 \right),\left( 2 \right),\left( 3 \right)\) là \(1 + 3 + 3 = 7\) nghiệm.

Chọn D.