Câu hỏi
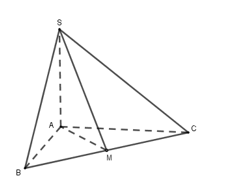
Cho hình chóp \(S.ABC\) có đường cao \(SA,\) tam giác \(ABC\) là tam giác cân tại \(A\) có \(AB = a,\widehat {BAC} = 120^\circ \). Biết thể tích khối chóp \(S.ABC\) bằng \(\dfrac{{\sqrt 3 {a^3}}}{24},\) góc giữa hai mặt phẳng \((SBC)\) và \((ABC)\) bằng
- A \(90^\circ \)
- B \(30^\circ \)
- C \(60^\circ \)
- D \(45^\circ \)
Phương pháp giải:
Để xác định góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) ta thực hiện các bước sau :
+ Xác định giao tuyến \(d\) của \(\left( P \right)\) và \(\left( Q \right).\)
+ Trong mặt phẳng \(\left( P \right)\) xác định đường thẳng \(a \bot d,\) trong mặt phẳng \(\left( Q \right)\) xác định đường thẳng \(b \bot d.\)
+ Khi đó góc giữa \(\left( P \right)\) và \(\left( Q \right)\) là góc giữa hai đường thẳng \(a\) và \(b.\)
Lời giải chi tiết:
Gọi \(M\) là trung điểm \(BC \Rightarrow AM \bot BC\) (do \(\Delta ABC\) cân tại \(A\))
Lại có \(\Delta SAB = \Delta SAC\,\,\,\left( {c.g.c} \right) \Rightarrow SB = SC\) hay \(\Delta SBC\) cân tại \(S\)
\( \Rightarrow SM \bot BC.\)
Ta có \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\AM \bot BC;\,\,\,AM \subset \left( {ABC} \right)\\SM \bot BC;\,\,SM \subset \left( {SBC} \right)\end{array} \right.\)
\( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SM;AM} \right) = \angle SMA\)
\({S_{\Delta ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat {BAC} = \dfrac{1}{2}{a^2}\sin {120^0} = \dfrac{{{a^2}\sqrt 3 }}{4}\).
Theo đề bài \({V_{S.ABC}} = \dfrac{{\sqrt 3 {a^3}}}{{24}} \Rightarrow \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{{{a^3}\sqrt 3 }}{{24}} \Leftrightarrow SA = \dfrac{{{a^3}\sqrt 3 }}{8}:\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{a}{2}.\)
Lại thấy \(\Delta ABM\) vuông tại \(M\) có \(AB = a;\,\,\,\angle ABM = \dfrac{{{{180}^0} - \angle BAC}}{2} = {30^0}\).
\( \Rightarrow AM = AB.\sin 30^\circ = \dfrac{a}{2}\).
Xét tam giác \(SAM\) vuông tại \(A\) có \(SA = AM = \dfrac{a}{2}\) nên \(\Delta SAM\) vuông cân tại \(A\) hay \(\angle SMA = {45^0}\)
Vậy góc giữa \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) là \(45^\circ .\)
Chọn D.