Phương pháp giải:

Áp dụng công thức tính tốc độ truyền sóng trên dây:\(\text{v = }\frac{\text{ }\!\!\lambda\!\!\text{ }}{\text{T}}\)

Từ khoảng cách AB ta tính được bước sóng. Khoảng thời gian mà độ lớn vận tốc dao động của của phần tử B nhỏ hơn vận tốc cực đại của phần tử M giúp xác định chu kì của dao động.

Lời giải chi tiết:

A là điểm nút và B là điểm bụng gần A nhất nên:

\(\text{AB = }\frac{\text{ }\!\!\lambda\!\!\text{ }}{\text{4}}\Rightarrow \text{ }\!\!\lambda\!\!\text{  = 4}\text{.AB = 18}\text{.4 = 72 (cm)}\)

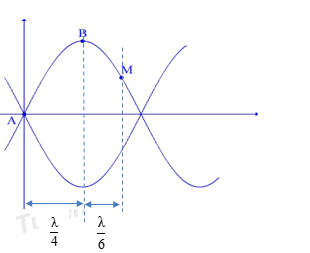
Điểm M cách B một khoảng: 12 cm \(=\frac{\text{ }\!\!\lambda\!\!\text{ }}{\text{6}}\)

\(\Rightarrow \) Biên độ dao động của điểm M: \({{\text{A}}_{\text{M}}}\text{ = }\frac{{{\text{A}}_{\text{B}}}}{\text{2}}\)\(\Rightarrow {{\text{v}}_{\text{Mmax}}}\text{=  }\!\!\omega\!\!\text{ }{{\text{A}}_{\text{M}}}\text{ = }\frac{\text{1}}{\text{2}}{{\text{v}}_{\text{Bmax}}}\)

\(\Rightarrow \) Khi phần tử B có vận tốc dao động bằng vận tốc cực đại của phần tử M, phần tử B có li độ: \(x=\frac{\sqrt{3}}{2}{{\text{A}}_{\text{B}}}\)

Do đó, trong một chu kì sóng, khoảng thời gian mà độ lớn vận tốc dao động của phân tử B nhỏ hơn vận tốc cực đại của phần tử M là:

\(\text{4}\text{.}\frac{\text{T}}{\text{12}}\text{ = }\frac{\text{T}}{\text{3}}\text{ = 0,1}\Rightarrow \text{T = 0,3 (s)}\)

\(\Rightarrow \text{v = }\frac{\text{ }\!\!\lambda\!\!\text{ }}{\text{T}}\text{ = }\frac{0,72}{0,3}\text{ = 2,4 (m/s)}\)

Chọn D