Câu hỏi
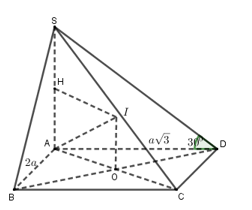
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, \(AB = 2a,AD = a\sqrt 3 \), cạnh bên \(SA\) vuông góc với mặt phẳng đáy, góc giữa \(SD\) và mặt phẳng đáy là \({30^0}\). Diện tích mặt cầu ngoại tiếp hình chóp là
- A \(8\pi {a^2}\)
- B \(\dfrac{{8\pi {a^2}}}{3}\)
- C \(4\pi {a^2}\)
- D \(\dfrac{{4\pi {a^2}}}{3}\)
Phương pháp giải:
- Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp.
- Tính diện tích theo công thức \(S = 4\pi {R^2}\).
Lời giải chi tiết:
Gọi \(O = AC \cap BD\).
Qua \(O\) dựng đường thẳng \(d\) vuông góc với đáy. Mặt phẳng trung trục của \(SA\) cắt \(d\) tại \(I\).
Khi đó \(I\) là tâm mặt cầu ngoại tiếp hình chóp.
Do \(SA \bot \left( {ABCD} \right)\) nên góc giữa \(SD\) và đáy bằng \(\widehat {SDA} = {30^0}\).
Tam giác \(SAD\) vuông tại \(A\) có \(AD = a\sqrt 3 ,\widehat {SDA} = {30^0}\) \( \Rightarrow SA = AD\tan {30^0} = a\sqrt 3 .\dfrac{{\sqrt 3 }}{3} = a\)
\( \Rightarrow AH = \dfrac{1}{2}AS = \dfrac{a}{2}\) ; \(AO = \dfrac{1}{2}AC = \dfrac{1}{2}\sqrt {A{D^2} + D{C^2}} = \dfrac{1}{2}\sqrt {3{a^2} + 4{a^2}} = \dfrac{{a\sqrt 7 }}{2}\)
\( \Rightarrow AI = \sqrt {A{O^2} + O{I^2}} = \sqrt {\dfrac{{7{a^2}}}{4} + \dfrac{{{a^2}}}{4}} = a\sqrt 2 \)\( \Rightarrow S = 4\pi A{I^2} = 4\pi .{\left( {a\sqrt 2 } \right)^2} = 8\pi {a^2}\).
Chọn A.