Câu hỏi
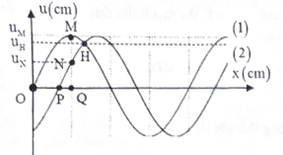
Một nguồn phát sóng cơ hình sin đặt tại O, truyền dọc theo sợi dây đàn hồi căng ngang rất dài OA với bước sóng 48cm. Tại thời điểm t1 và t2 hình dạng của một đoạn dây tương ứng như đường 1 và đường 2 của hình vẽ, trục Ox trùng với vị trí cân bằng của sợi dây, chiều dương trùng với chiều truyền sóng. Trong đó M là điểm cao nhất, uM, uN, uH lần lượt là li độ của các điểm M, N, H. Biết \(u_M^2 = u_N^2 + u_H^2\) và biên độ sóng không đổi. Khoảng cách từ P đến Q bằng:
- A 12cm
- B 2cm
- C 6cm
- D 4cm
Phương pháp giải:
Phương pháp:
Sử dụng kĩ năng đọc đồ thị và đường tròn lượng giác
Công thức tính độ lệch pha giữa hai điểm trên phương truyền sóng: \(\Delta \varphi = \frac{{2\pi d}}{\lambda }\)
Lời giải chi tiết:
Cách giải:
Biểu diễn vị trí các điểm tại các thời điểm t1 và t2 trên đường tròn lượng giác ta có:
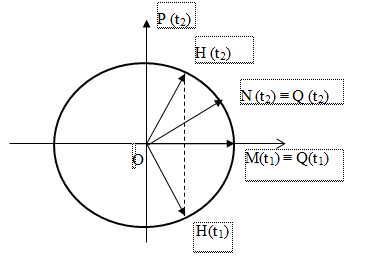
Theo bài ra ta có:
\(\begin{array}{l}u_M^2 = u_N^2 + u_H^2 \Leftrightarrow {A^2} = u_N^2 + u_H^2 \Leftrightarrow \frac{{u_N^2}}{{{A^2}}} + \frac{{u_H^2}}{{{A^2}}} = 1 \Rightarrow {u_N} \bot {u_H}\\ \Rightarrow \widehat {NOH} = \frac{\pi }{2}\,\,\,\left( 1 \right)\end{array}\)
Từ thời điểm t1 đến thời t2 H đi được góc 2α thì Q cũng đi được góc 2 (2)
Từ (1) và (2) \( \Rightarrow \widehat {NOM} = \frac{\pi }{3} \Rightarrow \widehat {PON} = \frac{\pi }{6} = \Delta {\varphi _{PQ}}\)
Mà: \(\Delta {\varphi _{PQ}} = \frac{{2\pi .PQ}}{\lambda } = \frac{\pi }{6} \Rightarrow PQ = \frac{\lambda }{{12}} = \frac{{48}}{{12}} = 4cm\)
Chọn D







