Câu hỏi
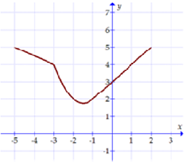
Cho hàm số \(f\left( x \right)\) liên tục có đồ thị như hình bên dưới.
Biết \(F'\left( x \right) = f\left( x \right),\,\forall x \in \left[ { - 5;2} \right]\) và \(\int\limits_{ - 3}^{ - 1} {f\left( x \right)dx} = \frac{{14}}{3}\). Tính \(F\left( 2 \right) - F\left( { - 5} \right)\).
- A \( - \frac{{145}}{6}\).
- B \( - \frac{{89}}{6}\).
- C \(\frac{{89}}{6}\).
- D \(\frac{{145}}{6}\).
Phương pháp giải:
Tính tích phân trên từng khoảng của các hàm số.
Lời giải chi tiết:
\(F\left( 2 \right) - F\left( { - 5} \right) = \int\limits_{ - 5}^2 {f\left( x \right)dx} = \int\limits_{ - 5}^{ - 3} {\frac{{5 - x}}{2}dx} + \int\limits_{ - 3}^{ - 1} {f\left( x \right)dx} + \int\limits_{ - 1}^2 {f\left( {x + 3} \right)dx} = \frac{{145}}{6}\).
Chọn: D
Câu hỏi trước
