Câu hỏi
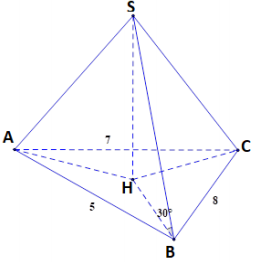
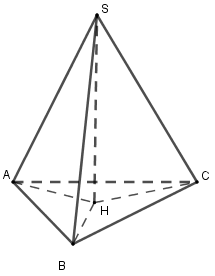
Cho hình chóp \(S.ABC\) có các cạnh bên \(SA,SB,SC\) tạo với đáy các góc bằng nhau và đều bằng \(30^\circ .\) Biết \(AB = 5;AC = 8;BC = 7,\) khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng
- A \(d = \frac{{35\sqrt {139} }}{{13}}\)
- B \(d = \frac{{35\sqrt {39} }}{{52}}\)
- C \(d = \frac{{35\sqrt {13} }}{{52}}\)
- D \(d = \frac{{35\sqrt {13} }}{{26}}\)
Phương pháp giải:
Sử dụng công thức Hê-rông tính diện tích tam giác \(ABC\) có ba cạnh \(a,b,c\) là \({S_{ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) với \(p = \frac{{a + b + c}}{2}\)
Sử dụng công thức diện tích \({S_{ABC}} = \frac{{abc}}{{4R}}\) với \(R\) là bán kính đường tròn ngoại tiếp \(\Delta ABC.\)
Sử dụng công thức thể tích khối chóp có chiều cao \(h\) và diện tích đáy \(S\) là \(V = \frac{1}{3}h.S \Leftrightarrow h = \frac{{3V}}{S}\)
Lời giải chi tiết:
Gọi \(H\) là chân đường vuông góc kẻ tuwg \(S\) đến mặt phẳng \(\left( {ABC} \right)\)
Khi đó từ giả thiết ta có \(\angle SAH = \angle SBH = \angle SCH = 30^\circ \)
Suy ra \(\Delta SAH = \Delta SBH = \Delta SCH\) (gn-cgv)
Suy ra \(HA = HB = HC\) hay \(H\) là tâm đường tròn ngoại tiếp \(\Delta ABC.\)
Tam giác \(ABC\) có \(AC = 7;AB = 5;BC = 8 \Rightarrow p = \frac{{AB + AC + BC}}{2} = 10\)
Theo công thức Hê-rông thì diện tích tam giác \(ABC\) là \({S_{ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)} = 10\sqrt 3 \)
Lại có \({S_{ABC}} = \frac{{AB.AC.BC}}{{4R}} \Rightarrow R = \frac{{5.7.8}}{{4S}} = \frac{{7\sqrt 3 }}{3}\) (với \(R\) là bán kính đường tròn ngoại tiếp \(\Delta ABC\))
Hay \(HA = \frac{{7\sqrt 3 }}{3}\) . Xét tam giác \(SHA\) vuông tại \(H\) có \(SH = \tan \widehat {SAH}.AH = \tan 30^\circ .\frac{{7\sqrt 3 }}{3} = \frac{7}{3}\)
Thể tích khối chóp \(S.ABC\) là \({V_{S.ABC}} = \frac{1}{3}SH.{S_{ABC}} = \frac{1}{3}.\frac{7}{3}.10\sqrt 3 = \frac{{70\sqrt 3 }}{9}\)
Lại có \(\Delta SHB\) vuông tại \(H\) nên \(SB = \frac{{SH}}{{\sin 30^\circ }} = \frac{{14}}{3} = SC\)
Xét tam giác \(SBC\) có \({p_1} = \frac{{SB + SC + BC}}{2} = \frac{{19}}{3}\) suy ra \({S_{\Delta SBC}} = \sqrt {{p_1}\left( {{p_1} - SB} \right)\left( {{p_1} - SC} \right)\left( {{p_1} - BC} \right)} = \frac{{8\sqrt {13} }}{3}\)
Từ đó \({V_{S.ABC}} = \frac{1}{3}d\left( {A,\left( {SBC} \right)} \right).{S_{\Delta SBC}} \Leftrightarrow d\left( {A,\left( {SBC} \right)} \right) = \frac{{3.{V_{S.ABC}}}}{{{S_{\Delta SBC}}}} = \frac{{3.\frac{{70\sqrt 3 }}{9}}}{{\frac{{8\sqrt {13} }}{3}}} = \frac{{35\sqrt {39} }}{{52}}.\)
Chọn B.