Phương pháp giải:

Sử dụng phương pháp hình học.

Lời giải chi tiết:

Theo bài ra ta có:

\(\begin{array}{l}z + 2 = iw \Rightarrow w = \dfrac{{z + 2}}{i}\\\left| {w - i} \right| = 2 \Rightarrow \left| {\dfrac{{z + 2}}{i} - i} \right| = 2 \Leftrightarrow \left| {z + 2 + 1} \right| = 2 \Leftrightarrow \left| {z + 3} \right| = 2\end{array}\)

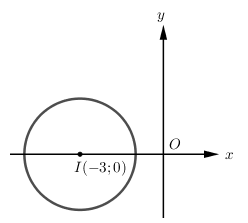
\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn \(I\left( { - 3;0} \right)\) bán kính \(R = 2\).

Gọi \(M\) là điểm biểu diễn số phức \(z\), dựa vào hình vẽ ta có:

\(\left\{ \begin{array}{l}{\left| z \right|_{\min }} \Leftrightarrow O{M_{\min }} \Leftrightarrow M\left( { - 1;0} \right) \Rightarrow {z_1} =  - 1\\{\left| z \right|_{\max }} \Leftrightarrow O{M_{\max }} \Leftrightarrow M\left( { - 5;0} \right) \Rightarrow {z_2} =  - 5\end{array} \right. \Rightarrow \left| {{z_1} + {z_2}} \right| = 6\).

Chọn C.