Câu hỏi
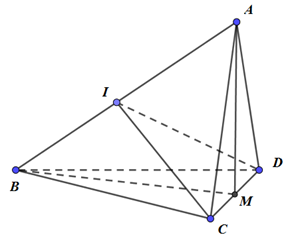
Cho tứ diện \(ABCD\) có \(\left( {ACD} \right) \bot \left( {BCD} \right),\,AC = AD = BC = BD = a,\,\,CD = 2x\). Giá trị của x để hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {ABD} \right)\) vuông góc với nhau là:
- A \(\frac{{a\sqrt 2 }}{3}\).
- B \(\frac{{a\sqrt 3 }}{3}\).
- C \(\frac{{a\sqrt 3 }}{2}\).
- D \(\frac{{a\sqrt 5 }}{3}\).
Phương pháp giải:
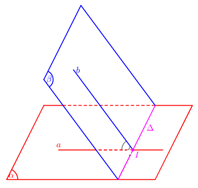
Xác định góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right):\)
- Tìm giao tuyến \(\Delta \) của \(\left( \alpha \right),\,\,\left( \beta \right)\).
- Xác định 1 mặt phẳng \(\left( \gamma \right) \bot \Delta \).
- Tìm các giao tuyến \(a = \left( \alpha \right) \cap \left( \gamma \right),b = \left( \beta \right) \cap \left( \gamma \right)\)
- Góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right):\,\,\angle \left( {\left( \alpha \right);\left( \beta \right)} \right) = \angle \left( {a;b} \right).\)
Lời giải chi tiết:
Gọi M là trung điểm của CD.
Do tam giác ACD và BCD là các tam giác cân tại A, B
\( \Rightarrow \left\{ \begin{array}{l}CD \bot AM\\CD \bot BM\end{array} \right. \Rightarrow CD \bot \left( {ABM} \right)\) và \(\angle \left( {\left( {ACD} \right);\left( {BCD} \right)} \right) = {90^0} = \angle AMB\)
Dễ dàng chứng minh được, \(\Delta ABC = \Delta ABD\left( {c.c.c} \right)\), dựng \(CI \bot AB\) tại I, suy ra \(DI \bot AB\,\,\, \Rightarrow \angle \left( {\left( {ABC} \right);\left( {ABD} \right)} \right) = \angle CID = {90^0}\)
\( \Rightarrow \Delta ICD\) vuông cân tại \(I \Rightarrow IM = CM = CD = \frac{{2x}}{2} = x\) (1)
Lại có: \(\Delta ABM\) vuông cân tại \(M,\,\,MI \bot AB\,\,\,\,\left( {do\,\,AB \bot \left( {ICD} \right)} \right)\)
\( \Rightarrow IM = \frac{{AM}}{{\sqrt 2 }} = \frac{{\sqrt {A{C^2} - C{M^2}} }}{{\sqrt 2 }} = \frac{{\sqrt {{a^2} - {x^2}} }}{{\sqrt 2 }}\) (2)
Từ (1), (2) suy ra: \(\frac{{\sqrt {{a^2} - {x^2}} }}{{\sqrt 2 }} = x \Leftrightarrow {a^2} - {x^2} = 2{x^2} \Leftrightarrow {x^2} = \frac{{{a^2}}}{3} \Leftrightarrow x = \frac{a}{{\sqrt 3 }}\).
Chọn: B