Phương pháp giải:

Biến đổi giả thiết để tìm được hàm \(f\left( x \right)\)

Đồ thị hàm số \(\dfrac{a}{{g\left( x \right)}}\) với \(a\) là hằng số \(\left( {a \ne 0} \right)\) có số tiệm cận đứng chính là số nghiệm của phương trình \(g\left( x \right) = 0.\)

Lời giải chi tiết:

Ta có \(f\left( {\tan x} \right) = {\cos ^4}x \Leftrightarrow f\left( {\tan x} \right) = {\left( {{{\cos }^2}x} \right)^2} = {\left( {\dfrac{1}{{1 + {{\tan }^2}x}}} \right)^2}\)

Đặt \(\tan x = u\) ta có \(f\left( u \right) = \dfrac{1}{{{{\left( {1 + {u^2}} \right)}^2}}} \Rightarrow f\left( x \right) = \dfrac{1}{{{{\left( {1 + {x^2}} \right)}^2}}}\)

Xét đồ thị hàm số \(g\left( x \right) = \dfrac{{2019}}{{f\left( x \right) - m}}\) có hai tiệm cận đứng khi \(f\left( x \right) - m = 0\) có hai nghiệm phân biệt

Hay \(f\left( x \right) = m\) có hai nghiệm phân biệt.

Ta có \(\dfrac{1}{{{{\left( {1 + {x^2}} \right)}^2}}} = m \Leftrightarrow {\left( {1 + {x^2}} \right)^2} = \dfrac{1}{m}\) (ĐK:\(m > 0\) do \(VT > 0\))

Xét hàm số \(g\left( x \right) = {\left( {1 + {x^2}} \right)^2} \Rightarrow g'\left( x \right) = 2.2x\left( {1 + {x^2}} \right) = 0 \Leftrightarrow x = 0\) Ta có BBT của \(g\left( x \right)\)

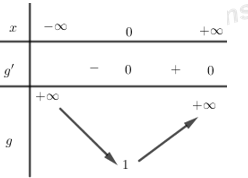
Ta thấy để \(f\left( x \right) = m\) có hai nghệm phân biệt thì \(\dfrac{1}{m} > 1 \Rightarrow 0 < m < 1\)

Chọn B.