Câu hỏi
Tại điểm O đặt hai nguồn âm điểm giống hệt nhau phát ra âm đẳng hướng có công suất không đổi. Điểm A cách O một đoạn x (m). Trên tia vuông góc với OA tại A lấy điểm B cách A một khoảng 6 m. Điểm M thuộc đoạn AB sao cho AM = 4,5 m. Thay đổi x để góc MOB có giá trị lớn nhất, khi đó mức cường độ âm tại A là LA = 40 dB. Để mức cường độ âm tại M là 50 dB thì cần đặt thêm tại O bao nhiêu nguồn âm nữa?
- A 33
- B 35
- C 15
- D 25
Phương pháp giải:
Áp dụng công thức tính mức cường độ âm \(L=10\lg \frac{I}{{{I}_{0}}}\)
Lời giải chi tiết:
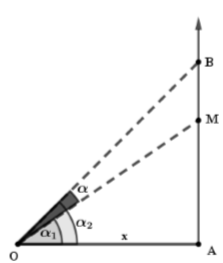
Từ hình vẽ ta có
\(\eqalign{
& \alpha = MOB = {\alpha _2} - {\alpha _1} \Leftrightarrow \tan \alpha = {{\tan {\alpha _2} - \tan {\alpha _1}} \over {1 + \tan {\alpha _2}.\tan {\alpha _1}}} = {{{{AB} \over x} - {{AM} \over x}} \over {1 + {{AB} \over x}.{{AM} \over x}}} \cr
& \Leftrightarrow \tan \alpha = {{{6 \over x} - {{4,} \over x}} \over {1 + {{6.4,5} \over {{x^2}}}}} = {{1,5} \over {x + {{27} \over x}}} = > {\alpha _{max}} \Leftrightarrow x = \sqrt {27} m = > \left\{ \matrix{
OB = 3\sqrt 7 m \hfill \cr
OM = 6,87m \hfill \cr} \right. \cr} \)
Khi tại O có 2 nguồn âm \(\frac{{{I}_{A}}}{{{I}_{M}}}={{\left( \frac{OM}{OA} \right)}^{2}}={{10}^{\frac{{{L}_{A}}-{{L}_{M}}}{10}}}\Leftrightarrow {{\left( \frac{6,87}{\sqrt{27}} \right)}^{2}}={{10}^{\frac{40-{{L}_{M}}}{10}}}=>{{L}_{M}}=37,57dB\)
Khi taijO có n nguồn âm và L’M = 50 dB
Ta có \(\frac{I{{'}_{M}}}{{{I}_{M}}}=\frac{n}{2}={{10}^{\frac{L{{'}_{M}}-{{L}_{M}}}{10}}}=\frac{n}{2}\Leftrightarrow \frac{n}{10}={{10}^{\frac{50-37,57}{10}}}\Leftrightarrow n=35\)
Vậy só nguồn âm cần đặt thêm tại O là 35 -2 – 33 ( nguồn)
Chọn A