Câu hỏi
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = {\left( {x - \sqrt 2 } \right)^2}{\left( {x + \sqrt 2 } \right)^2}\) trên đoạn \(\left[ { - \dfrac{1}{2};2} \right]\) là nghiệm của phương trình:
- A \({x^2} - 2x - 3 = 0\)
- B \({x^3} = - 2x + 3\)
- C \({x^2} - 4x = 0\)
- D \({{x}^{3}}=-2x+4\)
Phương pháp giải:
Sử dụng chức năng MODE 7 của máy tính CASIO.
Lời giải chi tiết:
Ta sử dụng chức năng MODE 7 của máy tính CASIO với thiết lập Start \( - \dfrac{1}{2}\); End 2 và Step \(\dfrac{5}{{38}}\) ta được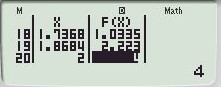 
và 
.
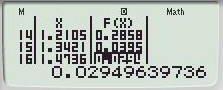\( \Rightarrow GTNN = 0\) và \(GTLN = 4\).
Trong 4 phương trình, ta thấy phương trình \({x^2} - 4x = 0\) có hai nghiệm \(x = 0\) và \(x = 4\).
Chọn C.
Câu hỏi trước
