Phương pháp giải:

Tính \(f'(x)\) và khảo sát hàm số, vẽ BBT để tìm GTLN và GTNN của hàm số.

Lời giải chi tiết:

Ta có: \(y = f\left( x \right) = \dfrac{{20}}{3} - \dfrac{{10x + 11}}{{3\left( {3{x^2} + 2x + 1} \right)}} = \dfrac{{20}}{3} - \dfrac{{10x + 11}}{{9{x^2} + 6x + 3}}\)

\( \Rightarrow f'\left( x \right) =  - \dfrac{{10\left( {9{x^2} + 6x + 3} \right) - \left( {18x + 6} \right)\left( {10x + 11} \right)}}{{{{\left( {9{x^2} + 6x + 3} \right)}^2}}} = \dfrac{{90{x^2} + 198x + 36}}{{{{\left( {9{x^2} + 6x + 3} \right)}^2}}}\)

\( \Rightarrow f'\left( x \right) = 0 \Leftrightarrow 90{x^2} + 198x + 36 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{1}{5}\\x =  - 2\end{array} \right.\)

Ta có BBT:

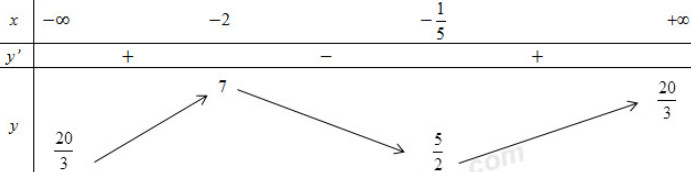
Theo BBT ta có: \(GTLN = 7\) và \(GTNN = \dfrac{5}{2}\).

Chọn C.