Phương pháp giải:

+) Phương trình \(f(x)=0\) có 4 nghiệm phân biệt nên hàm số có 3 điểm cực trị.

Lời giải chi tiết:

Ta có phương trình \(f\left( x \right) = 0\) có 4 nghiệm phân biệt \( \Rightarrow \) đồ thị hàm số \(y = f\left( x \right)\) cắt trục \(Ox\) tại 4 điểm phân biệt.

Khi đó đồ thị hàm số \(y=f(x)\) có 3 điểm cực trị.

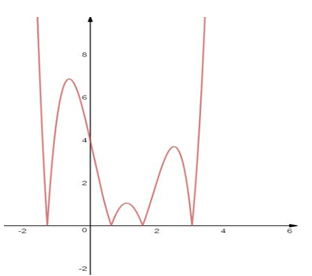
Khi đó dáng đồ thị của hàm số \(y = \left| {f\left( x \right)} \right|\) là:

Quan sát đồ thị hàm số ta thấy đồ thị hàm số có 7 điểm cực trị.

Chọn C.