Câu hỏi
Hàm số \(y = - {x^5} + {x^3} - 1\) nghịch biến trên khoảng nào trong các khoảng sau?
- A \(\left( { - \infty ; - \dfrac{{\sqrt 3 }}{{\sqrt 5 }}} \right)\) và \(\left( {\dfrac{{\sqrt 3 }}{{\sqrt 5 }}; + \infty } \right)\)
- B \(\left( { - \dfrac{{\sqrt 3 }}{{\sqrt 5 }};\dfrac{{\sqrt 3 }}{{\sqrt 5 }}} \right)\)
- C \(\left( { - \infty ; + \infty } \right)\)
- D \(\left( {\dfrac{{\sqrt 3 }}{{\sqrt 5 }}; + \infty } \right)\)
Phương pháp giải:
- Tính \(y'\) và kết luận các khoảng đơn điệu của hàm số.
Lời giải chi tiết:
Ta có: \(y'=-5{{x}^{4}}+3{{x}^{2}}\).
Hàm số nghịch biến thì \(y'\le 0\).
Nhập hàm y’ vào máy tính để thử với các giá trị tương ứng trong từng khoảng đáp án.
Thử với \(x=-1\) ta được \(y' = - 2 < 0\) \( \Rightarrow \) hàm số nghịch biến.
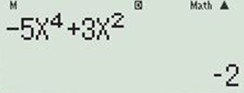
Thử với \(x=1\) ta được \(y'=-2<0\) \(\Rightarrow \) hàm số nghịch biến.
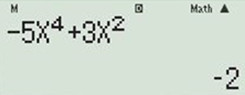
\(\Rightarrow \) Loại đáp án B và D.
Thử với \(x=\frac{7}{10}\) ta được \(y'=\frac{539}{2000}>0\) \( \Rightarrow \) hàm số đồng biến
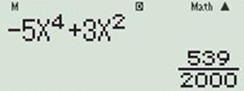
\(\Rightarrow \) loại đáp án C.
Chọn A.







