Câu hỏi
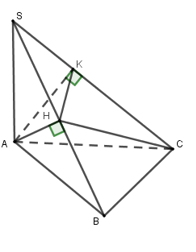
Cho tam giác \(ABC\) vuông tại \(B\) và nằm trong mặt phẳng \(\left( P \right)\) có \(AB = 2a,BC = 2\sqrt 3 a.\) Một điểm \(S\) thay đổi trên đường thẳng vuông góc với \(\left( P \right)\) tại \(A\,\left( {S \ne A} \right)\). Gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(A\) lên \(SB,SC\). Biết rằng khi \(S\) thay đổi thì bốn điểm \(A,B,H,K\) thuộc mặt cầu cố định. Tính bán kính \(R\) của mặt cầu đó.
- A \(R = 2a\)
- B \(R = \sqrt 3 a\)
- C \(R = \sqrt 2 a\)
- D \(R = a\)
Phương pháp giải:
Chỉ ra ba đỉnh \(H,K,B\) cùng nhìn cạnh \(AC\) dưới một góc vuông. Từ đó suy ra bán kính mặt cầu đi qua 4 điểm \(A,H,B,K.\)
Lời giải chi tiết:
Ta có \(\left\{ \begin{array}{l}BC \bot AB\left( {gt} \right)\\BC \bot SA\,\left( {do\,SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\) \( \Rightarrow BC \bot AH\)
mà \(AH \bot SB \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot HC\)
Ta thấy \(\widehat {AHC} = 90^\circ ;\,\widehat {AKC} = 90^\circ ;\widehat {ABC} = 90^\circ \) nên mặt cầu đi qua bốn đỉnh \(A;H;B;K\) nhận \(AC\) là đường kính nên bán kính \(R = \dfrac{{AC}}{2} = \dfrac{{\sqrt {A{B^2} + B{C^2}} }}{2} = \dfrac{{\sqrt {4{a^2} + 12{a^2}} }}{2} = 2a\) .
Chọn A.