Câu hỏi
Tìm x để \({x^3} - 4x + 3 > 0\).
- A \(x \in \left( {\dfrac{{ - 1 - \sqrt {13} }}{2};1} \right) \cup \left( {\dfrac{{ - 1 + \sqrt {13} }}{2}; + \infty } \right)\)
- B \(x > 1\)
- C \(x \in \left( {\dfrac{{ - 1 - \sqrt {13} }}{2};\dfrac{{ - 1 + \sqrt {13} }}{2}} \right)\)
- D \(x \in \left( { - \infty ;\dfrac{{ - 1 - \sqrt {13} }}{2}} \right) \cup \left( {\dfrac{{ - 1 + \sqrt {13} }}{2}; + \infty } \right)\)
Phương pháp giải:
+) Nhập hàm số \(y = {x^3} - 4x + 3\) vào máy tính Casio.
+) Sử dụng chức năng CALC để thử các đáp án.
Lời giải chi tiết:
Ta có: \({x^3} - 4x + 3 > 0\).
Ta nhập hàm \(y={{x}^{3}}-4x+3\) vào máy tính CASIO sau đó thử với các giá trị tương ứng với từng đáp án để chọn đáp án đúng nhất.
+) Đáp án A: thử với \(x=-2\) ta được \(y=3>0\)
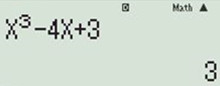
Thử với \(x=3\) ta được \(y=18>0\).
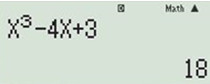
Đáp án A đúng.
Câu hỏi trước
