Câu hỏi
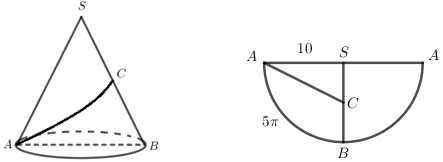
Tại trung tâm một thành phố người ta tạo điểm nhấn bằng cột trang trí hình nón có kích thước như sau: chiều dài đường sinh \(l = 10m\), bán kính đáy \(R = 5m\). Biết rằng tam giác \(SAB\) là thiết diện qua trục của hình nón và \(C\) là trung điểm \(SB\). Trang trí một hệ thống đèn điện tử chạy từ \(A\) đến \(C\) trên mặt nón. Xác định giá trị ngắn nhất của chiều dài dây đèn điện tử.
- A \(15m\)
- B \(10m\)
- C \(5\sqrt 3 m\)
- D \(5\sqrt 5 m\)
Phương pháp giải:
- Trải phẳng mặt nón cắt mép \(SA\).
- Tính góc ở tâm chắn cung \(AB\) và suy ra độ dài \(AC\) min.
Lời giải chi tiết:
Độ dài cung \(AB\) là \(\frac{{2\pi R}}{2} = \pi R = 5\pi \)
Có \(5\pi = 10.\angle ASC \Rightarrow \angle ASC = \frac{\pi }{2}\). Do đó \(A{C_{\min }} = \sqrt {S{A^2} + S{C^2}} = \sqrt {{{10}^2} + {5^2}} = 5\sqrt 5 \).
Chọn D.
Câu hỏi trước
