Câu hỏi
Một tứ diện đều cạnh a có một đỉnh trùng với đỉnh hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón. Khi đó diện tích xung quanh của hình nón bằng
- A \(\sqrt 3 \pi {a^2}\).
- B \(\dfrac{{\sqrt 3 }}{3}\pi {a^2}\).
- C \(\dfrac{{\sqrt 3 }}{2}\pi {a^2}\)
- D \(\dfrac{{2\sqrt 3 }}{3}\pi {a^2}\).
Phương pháp giải:
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\)
(Trong đó, \(r\): bán kính đáy, \(l\): độ dài đường sinh, h: độ dài đường cao).
Lời giải chi tiết:
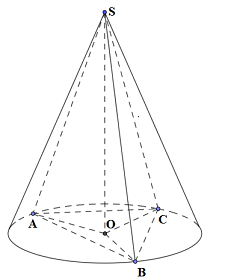
Hình nón có độ dài đường sinh \(l = SA = a\); bán kính đáy
\(r = OA = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\), có diện tích xung quanh là:
\({S_{xq}} = \pi rl = \pi .\dfrac{{a\sqrt 3 }}{3}.a = \dfrac{{\pi {a^2}\sqrt 3 }}{3}\).
Chọn: B
Câu hỏi trước
