Cách xác định tâm và tính bán kính đường tròn ngoại tiếp - Toán 9

Ta thường sử dụng các kiến thức

 - Sử dụng tính chất đường trung tuyến trong tam giác vuông: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền có độ dài bằng nửa cạnh huyền.

- Dùng định lí Pythagore:

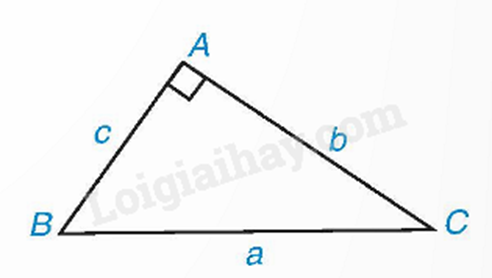
Trong tam giác ABC vuông tại A, ta có: \(B{C^2} = A{B^2} + A{C^2}\).

- Dùng hệ thức lượng về cạnh và góc trong tam giác vuông:

Trong tam giác ABC vuông tại A, ta có:

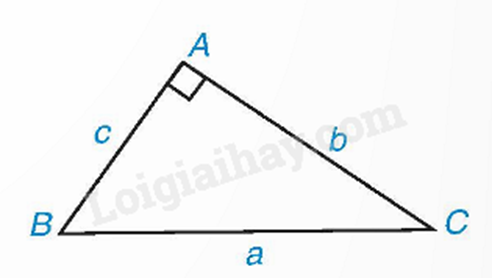
\(b = a.\sin B = a.\cos C;c = a.\sin C = a.\cos B.\)

\(b = c.\tan B = c.\cot C;c = b.\tan C = b.\cot B.\)

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.

Cạnh góc vuông = (cạnh huyền ) × (sin góc đối)

= (cạnh huyền ) × (cosin góc kề)

Ví dụ:

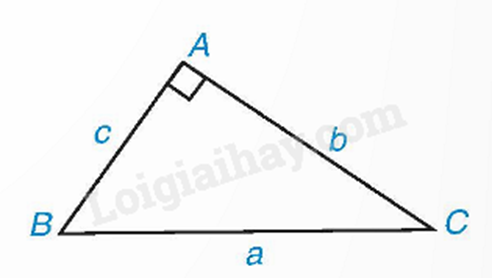
Trong tam giác ABC vuông tại A, ta có:

\(\begin{array}{l}b = a.\sin B = a.\cos C;\\c = a.\sin C = a.\cos B.\end{array}\)

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc côtang góc kề.

Cạnh góc vuông = (cạnh góc vuông còn lại ) × (tan góc đối) 

= (cạnh góc vuông còn lại ) × (cot góc kề)

Ví dụ:

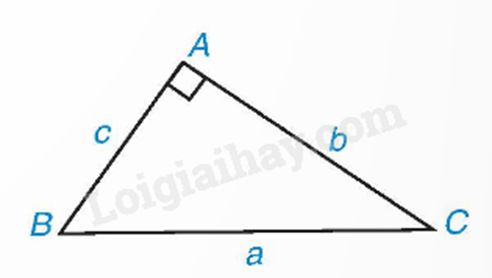
Trong tam giác ABC vuông tại A, ta có:

\(\begin{array}{l}b = c.\tan B = c.\cot C;\\c = b.\tan C = b.\cot B.\end{array}\)