1. Khái niệm hàm số y = ax²
Hàm số y = ax2, là một dạng của hàm số bậc hai, là hàm số có dạng như sau: \(y = a{x^2}\left( {a \ne 0} \right)\)
Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).
Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).
2. Khái niệm đồ thị của hàm số y = ax² (a ≠ 0)
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong được gọi là parabol. Parabol đó luôn đi qua gốc toạ độ và có dạng như sau:
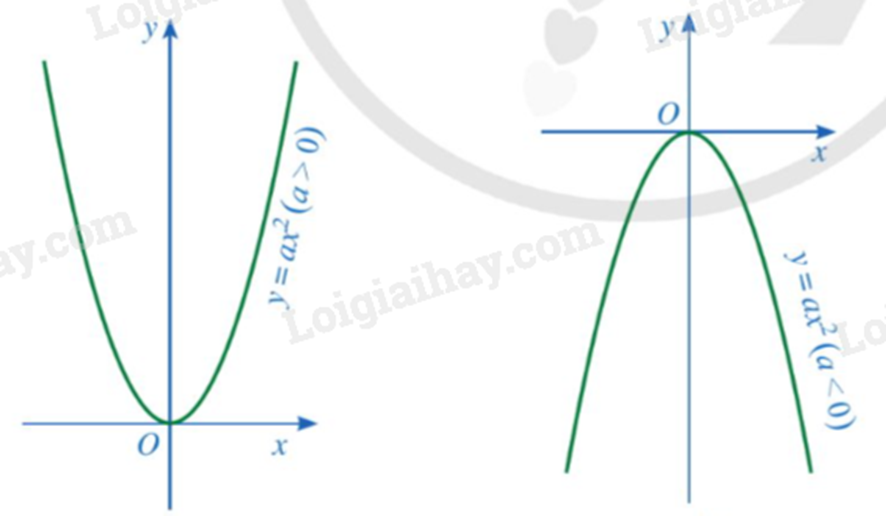
3. Trục đối xứng của đồ thị hàm số y = ax² (a ≠ 0)
Trục đối xứng của đồ thị hàm số y = ax² (a ≠ 0) là trục tung Oy.
Nhận xét: Do đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) nhận trục tung Oy là trục đối xứng nên ta có thể lập bảng giá trị của hàm số này với những giá trị x không âm và vẽ phần đồ thị tương ứng ở bên phải trục tung, sau đó lấy đối xứng phần đồ thị đã vẽ qua trục tung ta sẽ được đồ thị của hàm số đã cho.
4. Cách tạo công cụ vẽ đồ thị hàm số y = ax² (a ≠ 0) và trải nghiệm tính đối xứng trục của đồ thị hàm số đó
a) Tạo số a ban đầu
Nhập lệnh: a = 1 rồi bấm Enter
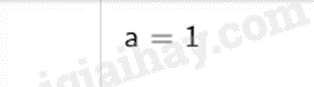
b) Tạo các hộp chọn đầu vào
Dùng  tạo hộp chọn đầu vào a và đặt tên là “Nhập vào số a (khác 0): a =” rồi tạo liên kết với a.
tạo hộp chọn đầu vào a và đặt tên là “Nhập vào số a (khác 0): a =” rồi tạo liên kết với a.

c) Vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) khi a thay đổi
- Nhập lệnh: y = ax^2 rồi bấm Enter
Khi đó màn hình sẽ xuất hiện đồ thị của hàm số \(y = a{x^2}\).
- Khi thay giá trị a ở hộp chọn đầu vào, màn hình sẽ xuất hiện đồ thị của hàm số \(y = a{x^2}\) tương ứng.
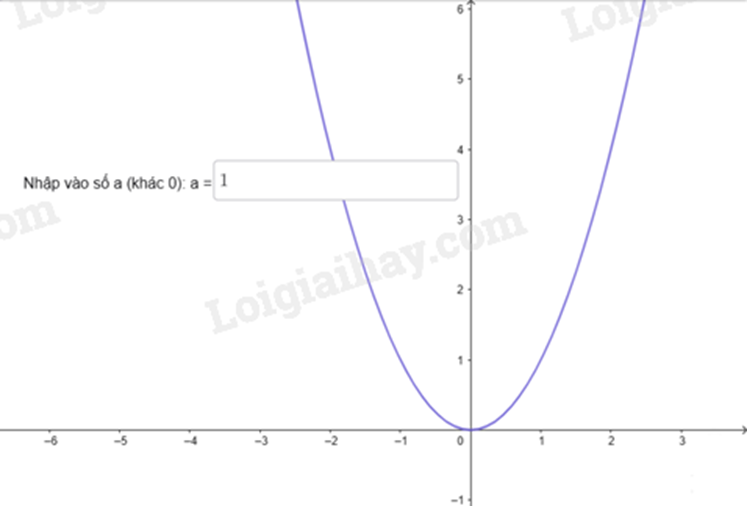
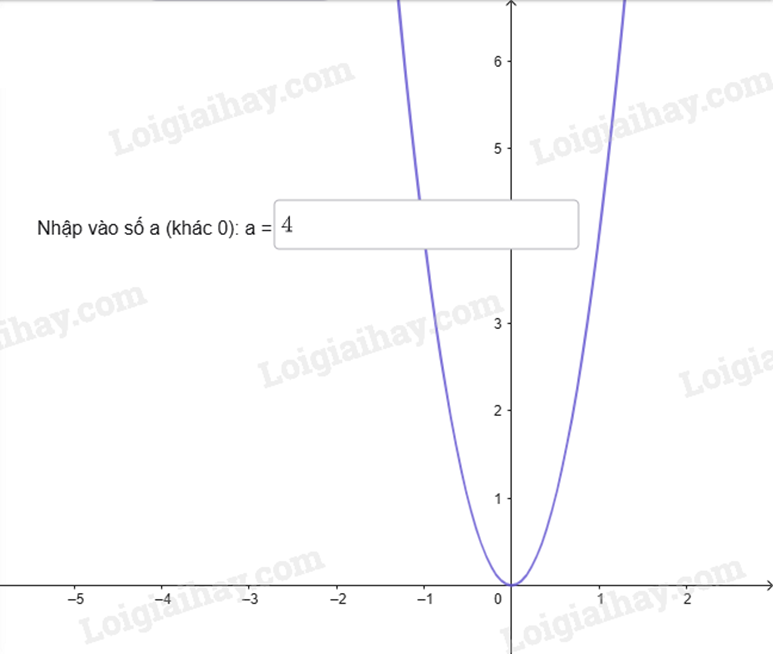
d) Trải nghiệm tính chất đối xứng trục của đồ thị hàm số \(y = a{x^2}\).
- Dùng  để vẽ một điểm A thuộc đồ thị của hàm số \(y = a{x^2}\).
để vẽ một điểm A thuộc đồ thị của hàm số \(y = a{x^2}\).
- Dùng  (lần lượt nháy chuột vào điểm A và trục Oy) để vẽ điểm A’ đối xứng với điểm A qua trục Oy (hình 1)
(lần lượt nháy chuột vào điểm A và trục Oy) để vẽ điểm A’ đối xứng với điểm A qua trục Oy (hình 1)
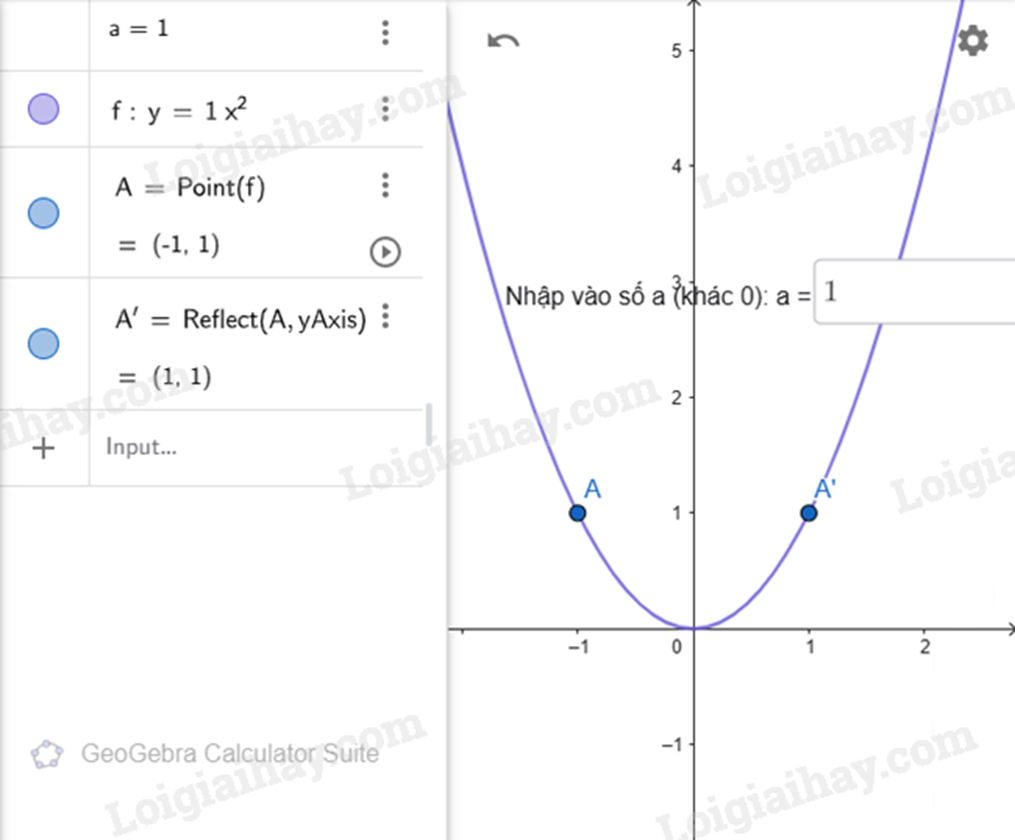
Khi thay giá trị a ở hộp chọn ban đầu vào hay di chuyển điểm A trên đồ thị của hàm số \(y = a{x^2}\), ta thấy điểm A’ luôn thuộc đồ thị của hàm số đó.

 Thực hành phần mềm Geogebra - Từ điển môn Toán 9
Thực hành phần mềm Geogebra - Từ điển môn Toán 9 






Danh sách bình luận