Cho tam giác $ABC$ cân tại $A$ và $\widehat A = 66^\circ $ nội tiếp đường tròn $\left( O \right)$. Trong các cung nhỏ $AB;BC;AC$, cung nào là cung lớn nhất?
-
A.
$AB$
-
B.
$AC$
-
C.
$BC$
-
D.
$AB,AC$
Sử dụng mối liên hệ giữa cung và dây
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+) Cung lớn hơn căng dây lớn hơn.
+) Dây lớn hơn căng cung lớn hơn.
+) Hai cung bằng nhau căng hai dây bằng nhau và ngược lại
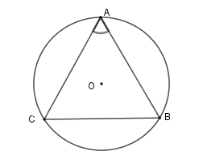
Vì tam giác $ABC$ cân tại $A$ có $\widehat A = 66^\circ \Rightarrow \widehat B = \widehat C = \dfrac{{180^\circ - \widehat A}}{2} = \dfrac{{180^\circ - 66^\circ }}{2} = 57^\circ $
Vì $\widehat A > \widehat B = \widehat C$ nên theo mối liên hệ giữa cạnh và góc trong tam giác ta có $BC > AB = AC$
Theo mối liên hệ giữa cung và dây ta có $\overparen{BC}$ $ > $ $\overparen{AB}$ $ = $ $\overparen{AC}$.
Đáp án : C
Các bài tập cùng chuyên đề
Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có dây $AB > CD$ khi đó
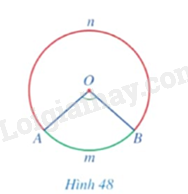
Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được phân chia bởi hai điểm A và B.
Quan sát góc ở tâm \(AOB\) (khác góc bẹt) ở Hình 48, cho biết trong hai phần đường tròn được tô màu xanh và màu đỏ, phần nào nằm bên trong, phần nào nằm bên ngoài góc \(AOB\).
Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có cung $MN < $ cung \(PQ\), khi đó
Chọn khẳng định đúng.
Chọn khẳng định sai.
Cho tam giác $ABC$ cân tại $A$ và $\widehat A = 70^\circ $ nội tiếp đường tròn $\left( O \right)$. Trong các cung nhỏ $AB;BC;AC$, cung nào là cung nhỏ nhất?
