Cho góc nhọn \(xOy.\) Điểm H nằm trên tia phân giác của góc \(xOy.\) Hạ \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) \(\left( {A \in {\rm{Ox}},\,B \in Oy} \right)\). Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.
Cho góc nhọn \(xOy.\) Điểm H nằm trên tia phân giác của góc \(xOy.\) Hạ \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) \(\left( {A \in {\rm{Ox}},\,B \in Oy} \right)\). Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.
Tam giác \(HAB\) là tam giác:
Tam giác \(HAB\) là tam giác:
đều
cân tại \(H\)
cân tại \(B\)
cân tại \(A\)
Đáp án: B
Tính chất các điểm nằm trên tia phân giác: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó. Từ đó chỉ ra hai cạnh \(HB = HA\).
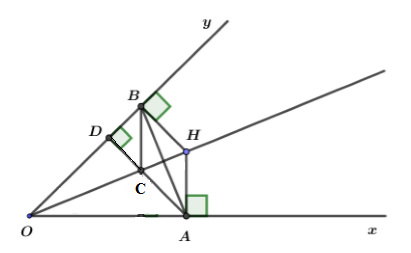
Vì \(H\) nằm trên tia phân giác của góc \(xOy\)
mà \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) nên ta có:
\(HA = HB\) (tính chất các điểm thuộc tia phân giác)
suy ra \(\Delta HAB\) cân tại \(H\).

Chọn câu đúng.
Chọn câu đúng.
\(OA = OB\)
\(OC\) là phân giác góc \(xOy\)
\(BC \,\bot \,{\rm{Ox}}\)
Cả A, B, C đều đúng
Đáp án: D
+) Chứng minh hai tam giác bằng nhau rồi suy ra cặp cạnh bằng nhau
+) Chứng minh C là trực tâm của tam giác \(OAB\).
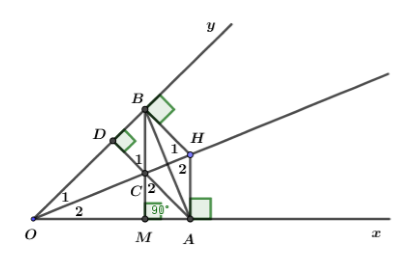
Xét hai tam giác vuông \(HBO\) và \(HAO\) ta có:
Cạnh huyền \(OH\,chung\)
Góc nhọn \({O_1} = {O_2}\)
suy ra \(\Delta HBO = \Delta HAO\,\) (cạnh huyền-góc nhọn)
Do đó: \(OA = OB\) (cạnh tương ứng)
Xét tam giác \(OAB\) cân tại O do \(OA = OB\) (cmt)
Mà \(AD \bot BO\) nên \(AD\) là đường cao.
C nằm trên tia phân giác góc O. Hay OC là đường phân giác góc O.
Trong một tam giác cân đường phân giác cũng chính là đường cao.
Mặt khác CO giao với AD tại C.
Suy ra \(C\) là trực tâm của tam giác OAB.
Do đó BC là đường cao.
Hay \(BC \bot OA\) hay \(BC \bot {\rm{Ox}}\)
Khi \(\widehat {xOy} = {60^0}\) thì ta có:
Khi \(\widehat {xOy} = {60^0}\) thì ta có:
\(OA = 2OD\)
\(OA = 3OD\)
\(3OA = 2OD\)
\(2OA = 3OD\)
Đáp án: A
Chứng minh khi \(\widehat {xOy} = {60^0}\) thì tam giác \({\rm N}OD\) là tam giác đều, từ đó suy ra \(OD = O{\rm N}\).
Sau đó lập luận để có mối quan hệ đúng.
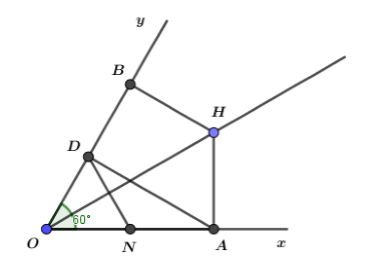
Gọi N là trung điểm của OA, khi đó trong tam giác vuông AOD (vuông tại D)
Khi đó \(D{\rm N} = O{\rm N} = \dfrac{{OA}}{2}\) (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Do đó \(\Delta {\rm N}OD\) cân tại N (1)
Mặt khác \(\widehat {AOD} = \widehat {xOy} = {60^0}\) (2)
Từ (1) và (2), suy ra \(\Delta {\rm N}OD\) là tam giác đều.
Do đó \(OD = O{\rm N}\) mà \(O{\rm N} = \dfrac{1}{2}OA\)
Nên \(OD = \dfrac{1}{2}OA\,\,hay\,\,OA = 2OD\).

Các bài tập cùng chuyên đề
Cho Hình 14. Tìm \(x\).
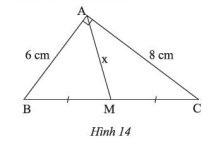
Cho tam giác \(ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Biết \(AB = 8\)cm; \(AC = 15\)cm. Độ dài đoạn \(AM\) là:
A. 8,5cm
B. 8cm
C. 7cm
D. 7,5cm
Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N lần lượt là hình chiếu của O trên AB, BC. Chứng minh: \(MN = \dfrac{1}{2}AC\)
Cho tam giác ABC có D là trung điểm cạnh AC. Biết \(AD = BD = CD = 5cm\) và \(BC = 6cm,\) tính độ dài cạnh AB.

1. Sử dụng tính chất tổng các góc của một tam giác bằng \({180^0}\) để chứng minh:
a) Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
b) Tam giác ABC có đường trung tuyến AM bằng nửa BC thì tam giác vuông tại A.
2. Sử dụng tính chất hai đường chéo của hình chữ nhật bằng nhau để chứng minh a), b) của ý 1.







Danh sách bình luận