Cho đường tròn \(\left( {O;8\,cm} \right).\) Dây \(AB\) và \(CD\) song song, có độ dài lần lượt là \(14cm\) và \(10\,cm\) .Tính khoảng cách giữa hai dây.
-
A.
\(2\sqrt {15} \,\left( {cm} \right)\)
-
B.
\(2\sqrt {39} \,\left( {cm} \right)\)
-
C.
\(\dfrac{{\sqrt {39} + \sqrt {15} }}{2}\,\left( {cm} \right)\)
-
D.
\(\sqrt {39} + \sqrt {15} \,\left( {cm} \right)\)
Sử dụng liên hệ giữa dây và đường kính: “Đường kính vuông góc với dây thì đi qua trung điểm của dây đó” để áp dụng định lý Pytago cho tam giác vuông phù hợp.
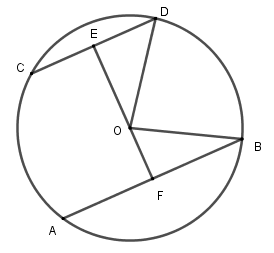
Kẻ đường thẳng qua \(O\) vuông góc với \(CD\) tại \(E\) và cắt \(AB\) tại \(F\) thì \(EF \bot AB\) vì \(AB\,{\rm{//}}\,CD\).
Khi đó \(E\) là trung điểm của \(CD\) và \(F\) là trung điểm của \(AB\) ( đường kính vuông góc với dây thì đi qua trung điểm dây đó). Nên \(ED = \dfrac{{CD}}{2} = 5cm;\,FB = \dfrac{{AB}}{2} = 7\,cm\); \(OD = OB = 8\,cm\)
Áp dụng định lý Pytago cho tam giác vuông \(OED\) ta được \(OE = \sqrt {O{D^2} - E{D^2}} = \sqrt {{8^2} - {5^2}} = \sqrt {39} \,cm\)
Áp dụng định lý Pytago cho tam giác vuông \(OFB\) ta được \(OF = \sqrt {O{B^2} - F{B^2}} = \sqrt {{8^2} - {7^2}} = \sqrt {15} \,cm\)
Vậy khoảng cách giữa hai dây là \(EF = OE + OF = \sqrt {39} + \sqrt {15} \,cm\).
Đáp án : D
Các bài tập cùng chuyên đề
Phát biểu nào sau đây là sai:
Cho đường tròn đường kính BC. Chứng minh rằng với điểm A bất kì (khác B và C) trên đườn tròn, ta đều có: BC < AB + AC < 2BC
Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó. Chứng minh rằng khoảng cách từ M đến AB không lớn hơn \(\frac{{AB}}{2}.\)
Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng:
a) Đường tròn đường kính BC đi qua các điểm H và K;
b) KH < BC.
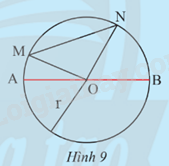
Trên đường tròn (O;R) lấy 4 điểm A, B, M, N sao cho AB đi qua O và MN không đi qua O (Hình 9).
a) Tính độ dài đoạn thẳng AB theo R.
b) So sánh độ dài của MN và OM + ON. Từ đó, so sánh độ dài của MN và AB.
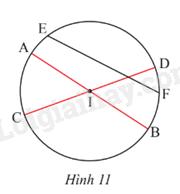
Cho đường tròn (I) có các dây cung AB, CD, EF. Cho biết AB và CD đi qua tâm I, EF không đi qua I (Hình 11). Hãy so sánh độ dài AB, CD, EF.
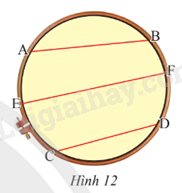
Bạn Mai căng ba đoạn chỉ AB, CD, EF có độ dài lần lượt là 16 cm, 14 cm và 20 cm trên một khung thêu hình tròn bán kính 10 cm (Hình 12). Trong ba dây trên, dây nào đi qua tâm của hình tròn? Giải thích.
Quan sát Hình 5.
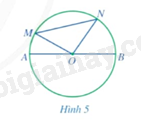
a) So sánh \(MN\) và \(OM + ON\).
b) So sánh \(MN\) và \(AB\).
Cho tam giác nhọn \(ABC\). Đường tròn tâm \(O\) đường kính \(BC\) cắt các cạnh \(AB\) và \(AC\) lần lượt tại \(M\) và \(N\). Chứng minh \(MN < BC\).
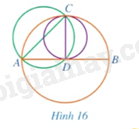
Trong Hình 16, có ba đường tròn với các đường kính lần lượt là \(AB,AC,CD\). Hãy sắp xếp độ dài ba đoạn thẳng \(AB,AC,CD\) theo thứ tự tăng dần và giải thích kết quả tìm được.
Chứng minh trong một đường tròn:
a) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy;
b) Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy;
c) Hai dây bằng nhau thì cách đều tâm;
d) Hai dây cách đều tâm thì bằng nhau.
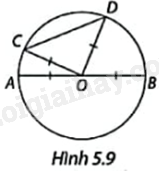
Trong Hình 5.9, lần lượt so sánh độ dài dây CD, đường kính AB với tổng độ dài \(OC + OD\), em hãy cho biết trong hai dây AB và CD, dây nào dài hơn?
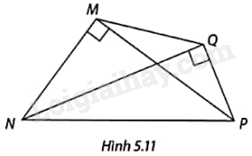
So sánh độ dài hai cạnh MQ và NP trong Hình 5.11.
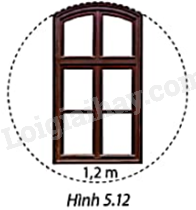
Cửa sổ được thiết kế với phần vòm bên trên là một phần của một đường tròn (Hình 5.12). Nếu chiều rộng cửa là 1,2m thì bán kính của đường tròn nói trên ít nhất bằng bao nhiêu mét?
Vận động viên X chạy trên một đường chạy có dạng đường tròn bán kính 50m xuất phát từ vị trí A. Khoảng cách lớn nhất từ vận động viên đến điểm A là bao nhiêu mét?
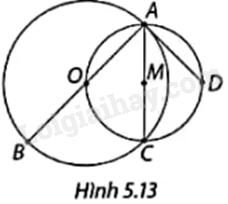
Sắp xếp các đoạn thẳng AB, AC và AD trong Hình 5.13 theo thứ tự tăng dần về độ dài và giải thích.
Cho đường tròn (O) đường kính AB. Dây CD vuông góc với AB tại điểm M khác điểm O.
Trong các khẳng định sau, khẳng định nào sai?
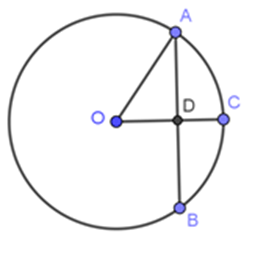
Trong hình vẽ bên cho $OC \bot AB,AB = 12cm,OA = 10cm$. Độ dài $AC$ là:
Cho đường tròn $\left( O \right)$ đường kính $AB$ và dây $CD$ không đi qua tâm. Khẳng định nào sau đây là đúng?
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ không đi qua tâm. Biết rằng khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng?
Cho đường tròn \(\left( O \right)\)có hai dây \(AB,CD\) không đi qua tâm. Biết rằng khoảng cách từ tâm \(O\) đến dây \(AB\) lớn hơn khoảng cách từ tâm \(O\) đến dây \(CD\). Kết luận nào sau đây là đúng?
“Trong một đường tròn, đường kính đi qua trung điểm một dây không đi qua tâm thì $ \ldots $với dây ấy”. Điền vào dấu $...$ cụm từ thích hợp.
“Trong một đường tròn, đường kính vuông góc với dây thì …của dây ấy”. Điền vào dấu \(...\) cụm từ thích hợp.
Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn
Chọn khẳng định đúng trong các khẳng định sau. Trong hai dây của một đường tròn
Cho đường thẳng \(d\) cắt đường tròn \(\left( O \right)\) tại hai điểm phân biệt \(A;\,\,B.\) Biết khoảng cách từ điểm \(O\) đến đường thẳng \(d\) bằng \(3cm\) và độ dài đoạn thẳng \(AB\) bằng \(8cm.\) Bán kính của đường tròn \(\left( O \right)\) bằng:
Cho đường tròn $\left( {O;R} \right)$có hai dây $AB,CD$ bằng nhau và vuông góc với nhau tại $I$. Giả sử $IA = 2cm;IB = 4cm$ . Tổng khoảng cách từ tâm $O$ dây $AB,CD$ là
Cho đường tròn \(\left( {O;R} \right)\) có hai dây \(AB,CD\) bằng nhau và vuông góc với nhau tại \(I\) . Giả sử \(IA = 6cm;IB = 3cm\) . Tổng khoảng cách từ tâm \(O\) dây \(AB,CD\) là
Cho đường tròn $\left( {O;R} \right)$có hai dây $AB,CD$ vuông góc với nhau ở $M$. Biết$AB = 16\,cm;\,CD = 12\,cm;\,MC = 2\,cm$. Khoảng cách từ tâm $O$ đến dây $AB$ là
Cho đường tròn \(\left( {O;R} \right)\) có hai dây \(AB,CD\) vuông góc với nhau ở \(M\). Biết\(\,CD = 8\,cm;\,MC = 1\,cm\). Khoảng cách từ tâm \(O\) đến dây \(AB\) là
