Có bao nhiêu giá trị nguyên của m để phương trình \({x^2} - 4\sqrt {{x^2} + 1} - \left( {m - 1} \right) = 0\) có \(4\) nghiệm phân biệt
-
A.
\(1\).
-
B.
\(0\).
-
C.
\(2\).
-
D.
Vô số.
- Đặt ẩn phụ \(t = \sqrt {{x^2} + 1} \), tìm điều kiện của \(t\)
- Biến đổi phương trình về bậc hai ẩn \(t\) và tìm điều kiện để phương trình có nghiệm thỏa mãn yêu cầu bài toán (sử dụng phương pháp hàm số)
Điều kiện xác định \(x \in \mathbb{R}\).
Đặt \(t = \sqrt {{x^2} + 1} \), \(t \ge 1\).
Phương trình trở thành \({t^2} - 1 - 4t - m + 1 = 0\)\( \Leftrightarrow {t^2} - 4t = m\). \(\left( 2 \right)\)
Để phương trình có \(4\) nghiệm phân biệt thì phương trình \(\left( 2 \right)\) có hai nghiệm phân biệt lớn hơn \(1\).
Xét hàm số \(f\left( t \right) = {t^2} - 4t\) có đồ thị là parabol có hoành độ đỉnh \(x = 2 \in \left( {1; + \infty } \right)\) nên ta có bảng biến thiên:
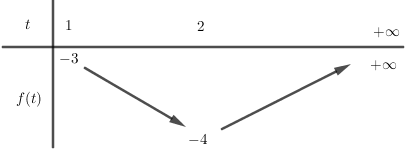
Dựa BBT ta thấy để $(2)$ có hai nghiệm phân biệt lớn hơn $1$ thì \( - 4 < m < - 3\).
Vậy không có giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán.
Đáp án : B
Một số em có thể sẽ nhận cả giá trị $-3$ vì nghĩ rằng phương trình $(2)$ vẫn có $2$ nghiệm phân biệt mà không chú ý rằng khi đó phương trình đã cho sẽ chỉ có $3$ nghiệm, trong đó có $1$ nghiệm $x=0$








Danh sách bình luận