Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}3} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}4} \right)^2}\; = {\rm{ }}25\) và đường thẳng \(\Delta :{\rm{ }}2x{\rm{ }} + {\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
a) Tìm ảnh của (C) và \(\Delta \) qua phép đối xứng trục Ox.
b) Tìm ảnh của (C) và \(\Delta \) qua phép đối xứng trục Oy.
c) Tìm ảnh của (C) và \(\Delta \) qua phép đối xứng trục \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0\).
Nếu \(M' = {Đ_{Ox}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Nếu \(M' = {Đ_{Oy}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = - {x_M}\\{y_{M'}} = {y_M}\end{array} \right.\)
Đường tròn (C) có tâm I(3; 4), bán kính R = 5.
a)
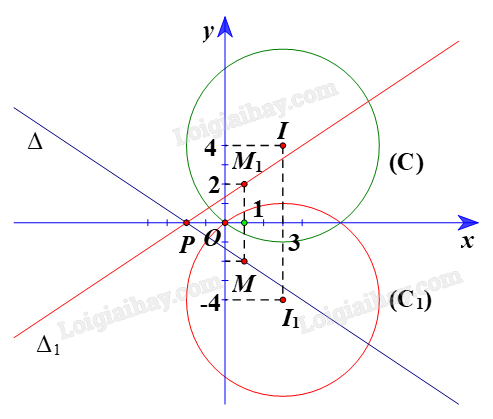
+ Gọi \(({C_1})\) là ảnh của (C) qua \({Đ_{Ox}}\), khi đó (C1) có tâm I1 là ảnh của I(3; 4) \({Đ_{Ox}}\) và bán kính \({R_1}\; = {\rm{ }}R{\rm{ }} = {\rm{ }}5.\)
Ta có \({I_1}\; = {\rm{ }}{Đ_{Ox}}\left( I \right).\)
Suy ra Ox là đường trung trực của đoạn \(\;I{I_1}\)
Do đó hai điểm I(3; 4) và I1 có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ \({I_1}\left( {3;{\rm{ }}-4} \right).\)
Vậy ảnh của đường tròn (C) qua ĐOx là đường tròn (C1) có phương trình là:
\({\left( {x{\rm{ }}-{\rm{ }}3} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}4} \right)^2}\; = {\rm{ }}25.\)
+ Trục \(Ox:{\rm{ }}y{\rm{ }} = {\rm{ }}0.\)
Với y = 0, ta có \(2x{\rm{ }} + {\rm{ }}3.0{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0 \Leftrightarrow x{\rm{ }} = {\rm{ }}-2.\)
Suy ra giao điểm của ∆ và trục Ox là điểm \(P\left( {-2;{\rm{ }}0} \right).\)
Khi đó \(P{\rm{ }} = {\rm{ }}{Đ_{Ox}}\left( P \right).\)
Chọn \(M\left( {1;{\rm{ }}-2} \right) \in \Delta \)
Gọi M1 và ∆1 theo thứ tự là ảnh của M và \(\Delta \) qua \({Đ_{Ox}}\)
Ta thấy Ox là đường trung trực của đoạn MM1.
Do đó hai điểm M(1; –2) và M1 có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ \({M_1}\left( {1;{\rm{ }}2} \right).\)
Ta có \(\overrightarrow {{M_1}P} = \left( { - 3; - 2} \right)\)
Đường thẳng \({\Delta _1}\;\) có vectơ chỉ phương \(\overrightarrow {{M_1}P} = \left( { - 3; - 2} \right)\)
Suy ra \({\Delta _1}\;\) có vectơ pháp tuyến \({\vec n_{{\Delta _1}}} = \left( {2; - 3} \right)\)
Vậy đường thẳng \({\Delta _1}\;\) đi qua P(–2; 0) và có vectơ pháp tuyến \({\vec n_{{\Delta _1}}} = \left( {2; - 3} \right)\) nên có phương trình là:
\(2\left( {x{\rm{ }} + {\rm{ }}2} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }}-{\rm{ }}0} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow 2x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
b)

+ Gọi \(({C_2})\) là ảnh của (C) qua \({Đ_{Oy}}\), khi đó \(({C_2})\) có tâm \({I_{2\;}}\) là ảnh của \(I\left( {3;{\rm{ }}4} \right)\)qua \({Đ_{Oy}}\) và bán kính \({R_2}\; = {\rm{ }}R{\rm{ }} = {\rm{ }}5.\)
Ta có \({I_2}\; = {\rm{ }}{Đ_{Oy}}\left( I \right).\)
Suy ra Oy là đường trung trực của đoạn \(I{I_2}.\)
Do đó hai điểm I(3; 4) và \({I_{2\;}}\) có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ \({I_2}\left( {-3;{\rm{ }}4} \right).\)
Vậy ảnh của đường tròn (C) qua \({Đ_{Oy}}\) là đường tròn \(({C_2})\) có phương trình là:
\({\left( {x{\rm{ }} + {\rm{ }}3} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}4} \right)^2}\; = {\rm{ }}25.\)
+ Trục \(Oy:{\rm{ }}x{\rm{ }} = {\rm{ }}0.\)
Với x = 0, ta có \(2.0{\rm{ }} + {\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0{\rm{ }} \Leftrightarrow y = - \frac{4}{3}\)
Suy ra giao điểm của \(\Delta \) và trục Oy là điểm \(Q\left( {0; - \frac{4}{3}} \right)\)
Khi đó \(Q{\rm{ }} = {\rm{ }}{Đ_{Oy}}\left( Q \right).\)
Chọn \(M\left( {1;{\rm{ }}-2} \right) \in \Delta \)
Gọi \({M_2}\;\) và \({\Delta _2}\;\) theo thứ tự là ảnh của M và \(\Delta \) qua \({Đ_{Oy}}\)
Ta thấy Oy là đường trung trực của đoạn \(M{M_2}.\)
Do đó hai điểm M(1; –2) và M2 có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ \({M_2}\left( {-1;{\rm{ }}-2} \right).\)
Ta có \(\overrightarrow {{M_2}Q} = \left( {1;\frac{2}{3}} \right)\)
Đường thẳng ∆2 có vectơ chỉ phương \({\vec u_2} = 3\overrightarrow {{M_2}Q} = \left( {3;2} \right)\)
Suy ra ∆2 có vectơ pháp tuyến \({\vec n_{{\Delta _2}}} = \left( {2; - 3} \right)\)
Vậy đường thẳng \({\Delta _2}\) đi qua \({M_2}\left( {-1;{\rm{ }}-2} \right)\) và có vectơ pháp tuyến \({\vec n_{{\Delta _2}}} = \left( {2; - 3} \right)\) nên có phương trình là:
\(2\left( {x{\rm{ }} + {\rm{ }}1} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow 2x{\rm{ }}-{\rm{ }}3y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
c)
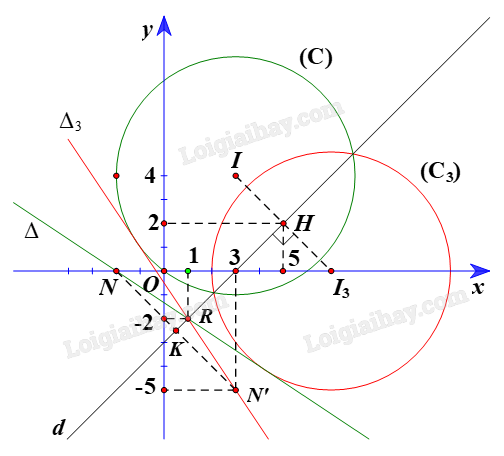
+ Gọi \({\rm{ }}({C_3})\) là ảnh của (C) qua \({Đ_d}\), khi đó \(({C_2})\) có tâm \({I_3}\) là ảnh của I(3; 4) qua Đd và bán kính \({R_3}\; = {\rm{ }}R{\rm{ }} = {\rm{ }}5.\)
Ta có \({I_3}\; = {\rm{ }}{Đ_d}\left( I \right).\)
Suy ra d là đường trung trực của đoạn II3 nên II3 ⊥ d tại trung điểm của II3.
Mà đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\vec n_d} = \left( {1; - 1} \right)\)
Suy ra đường thẳng II3 có vectơ chỉ phương \({\vec n_d} = \left( {1; - 1} \right)\)
Do đó đường thẳng II3 có vectơ pháp tuyến \(\vec u = \left( {1;1} \right)\)
Vì vậy đường thẳng II3 đi qua điểm I(3; 4) và nhận \(\vec u = \left( {1;1} \right)\) làm vectơ pháp tuyến nên có phương trình là:
\(1\left( {x{\rm{ }}-{\rm{ }}3} \right){\rm{ }} + {\rm{ }}1\left( {y{\rm{ }}-{\rm{ }}4} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\)
Gọi H là giao điểm của \(I{I_3}\) và đường thẳng d.
Suy ra tọa độ H thỏa mãn hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{{\rm{x}} - {\rm{y}} - 3 = 0}\\{{\rm{x}} + {\rm{y}} - 7 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{x}} = 5}\\{{\rm{y}} = 2}\end{array}} \right.\)
Do đó tọa độ \(H\left( {5;{\rm{ }}2} \right).\)
Ta có H là trung điểm \(I{I_3}.\)
Suy ra \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_{{{\rm{I}}_3}}} = 2{{\rm{x}}_{\rm{H}}} - {{\rm{x}}_{\rm{I}}} = 2.5 - 3 = 7}\\{{{\rm{y}}_{{{\rm{I}}_3}}} = 2{{\rm{y}}_{\rm{H}}} - {{\rm{y}}_{\rm{I}}} = 2.2 - 4 = 0}\end{array}} \right.\)
Do đó tọa độ \({I_3}\left( {7;{\rm{ }}0} \right).\)
Vậy ảnh của đường tròn (C) qua \({Đ_d}\) là đường tròn \(({C_3})\) có phương trình là:
\({\left( {x{\rm{ }}-{\rm{ }}7} \right)^2}\; + {\rm{ }}{y^2}\; = {\rm{ }}25.\)
+ Gọi R là giao điểm của \(\Delta \) và d.
Suy ra tọa độ R thỏa mãn hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{2{\rm{x}} + 3{\rm{y}} + 4 = 0}\\{{\rm{x}} - {\rm{y}} - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{x}} = 1}\\{{\rm{y}} = - 2}\end{array}} \right.\)
Do đó tọa độ R(1; –2).
Khi đó \(R{\rm{ }} = {\rm{ }}{Đ_d}\left( R \right).\)
Chọn \(N\left( {-2;{\rm{ }}0} \right) \in \Delta :{\rm{ }}2x{\rm{ }} + {\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
Gọi N’ và \({\Delta _3}\) theo thứ tự là ảnh của N và \(\Delta \) qua \({Đ_d}\).
Ta thấy d là đường trung trực của đoạn NN’.
Mà đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\vec n_d} = \left( {1; - 1} \right)\)
Suy ra đường thẳng NN’ có vectơ chỉ phương \({\vec n_d} = \left( {1; - 1} \right)\)
Do đó đường thẳng NN’ có vectơ pháp tuyến \(\vec u = \left( {1;1} \right)\)
Vì vậy đường thẳng NN’ đi qua N(–2; 0) và nhận \(\vec u = \left( {1;1} \right)\) làm vectơ pháp tuyến nên có phương trình là:
\(1\left( {x{\rm{ }} + {\rm{ }}2} \right){\rm{ }} + {\rm{ }}1\left( {y{\rm{ }}-{\rm{ }}0} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x{\rm{ }} + {\rm{ }}y{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}0.\)
Gọi K là giao điểm của NN’ và đường thẳng d.
Suy ra tọa độ K thỏa mãn hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{{\rm{x}} + {\rm{y}} + 2 = 0}\\{{\rm{x}} - {\rm{y}} - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{x}} = \frac{1}{2}}\\{{\rm{y}} = - \frac{5}{2}}\end{array}} \right.\)
Do đó tọa độ \(K\left( {\frac{1}{2}; - \frac{5}{2}} \right)\)
Ta có K là trung điểm NN’.
Suy ra \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_{{\rm{N'}}}} = 2{{\rm{x}}_{\rm{K}}} - {{\rm{x}}_{\rm{N}}} = 2.\frac{1}{2} + 2 = 3}\\{{{\rm{y}}_{{\rm{N'}}}} = 2{{\rm{y}}_{\rm{K}}} - {{\rm{y}}_{\rm{N}}} = 2.\left( { - \frac{5}{2}} \right) - 0 = - 5}\end{array}} \right.\)
Do đó tọa độ N’(3; –5).
Với R(1; –2), ta có \(\overrightarrow {N'R} = \left( { - 2;3} \right)\)
Đường thẳng \({\Delta _3}\) có vectơ chỉ phương \(\overrightarrow {N'R} = \left( { - 2;3} \right)\)
Suy ra \({\Delta _3}\) có vectơ pháp tuyến \({\vec n_{{\Delta _3}}} = \left( {3;2} \right)\)
Vậy đường thẳng \({\Delta _3}\) đi qua N’(3; –5) và nhận \({\vec n_{{\Delta _3}}} = \left( {3;2} \right)\) làm vectơ pháp tuyến nên có phương trình là:
\(3\left( {x{\rm{ }}-{\rm{ }}3} \right){\rm{ }} + {\rm{ }}2\left( {y{\rm{ }} + {\rm{ }}5} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow 3x{\rm{ }} + {\rm{ }}2y{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0.\)

Các bài tập cùng chuyên đề
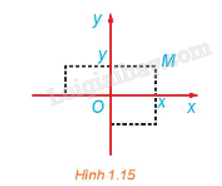
Xét mặt phẳng tọa độ Oxy (H.1.15). Trong các khẳng định sau, chọn các khẳng định đúng.
a) Phép đối xứng trục Ox biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\) thành điểm có tọa độ \(\left( {x;{\rm{ }}-{\rm{ }}y} \right).\)
b) Phép đối xứng trục Oy biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\) thành điểm có tọa độ \(\left( {-{\rm{ }}x;{\rm{ }}y} \right).\)
c) Phép đối xứng trục Ox biến A(1; 2) thành điểm \(A'\left( {-{\rm{ }}1;{\rm{ }}-{\rm{ }}2} \right).\)
Cầu Ponte Sisto in hình dưới dòng sông Tiber, tạo nên một hình ảnh có tính đối xứng trục.

a) Hãy chỉ ra trục đối xứng của hình ảnh đó.
b) Có thể đếm được bao nhiêu hình bóng điện dưới sông? Mỗi hình đó là ảnh dưới sông của bóng điện nào trên cầu?
Bằng quan sát, hãy cho biết, trong hai hình ảnh bên, hình nào có trục đối xứng.

Cho đường thẳng \(\Delta \) và hai điểm A, B, sao cho \(\Delta \) không phải là đường trung trực của đoạn thẳng AB. Điểm M thay đổi trên \(\Delta \) (M không thuộc đường thẳng AB). Gọi M' là điểm sao cho A, B, M, M' là 4 đỉnh của một hình thang cân nhận AB là một cạnh đáy. Chứng minh rằng M' thay đổi trên một đường thẳng cố định.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – y – 1 = 0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép đối xứng trục Ox.
Cho phép đối xứng trục d biến M thành M', N thành N'. Xét hệ trục tọa độ Oxy sao cho trục Oy trùng với d (H.1.16a). Giả sử M có tọa độ là \(\left( {{x_1};{\rm{ }}{y_1}} \right),\) N có tọa độ là \(\left( {{x_2};{\rm{ }}{y_2}} \right).\)
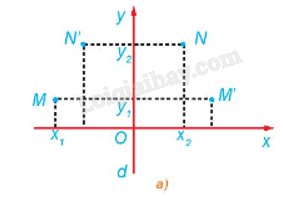
a) Hãy cho biết tọa độ của M', N'.
b) Tính \(M{N^2},{\rm{ }}M'N{'^2}\;\) theo tọa độ của các điểm tương ứng.
c) So sánh độ dài các đoạn thẳng MN, M'N'.
Cho hai điểm phân biệt A và B. Xác định phép đối xứng trục biến điểm A thành điểm B.
Cho hai đường tròn không đồng tâm, những có cùng bán kính (O1; R) và (O2; R). Xác định phép đối xứng trục biến (O1; R) thành (O2; R).
Cho đường thẳng d và hai điểm phân biệt A, B sao cho đường thẳng AB không vuông góc với d. Gọi M, N tương ứng là các điểm đối xứng với A, B qua d. Hỏi A, B, M, N có là 4 đỉnh của một hình thang cân hay không?
Trong mặt phẳng tọa độ Oxy, cho \(\Delta \): x + 2y – 1 = 0. Viết phương trình đường thẳng d đối xứng với \(\Delta \) qua trục Ox.
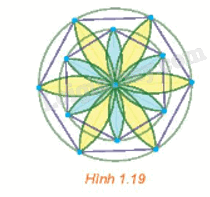
Dùng com-pa, thước kẻ, bút, hãy vẽ lại các nét thẳng và tròn trong Hình 1.19.
Cho một mảnh giấy hình thang cân ABCD (AB // CD). Hãy chỉ ra một cách cắt mảnh giấy đó thành hai mảnh giấy bằng nhau.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\Delta :{\rm{ }}2x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}0\) và hai điểm \(A\left( {-{\rm{ }}1;{\rm{ }}2} \right),{\rm{ }}B\left( {-{\rm{ }}3;{\rm{ }}4} \right).\)
a) Tìm tọa độ điểm \(A'\) là ảnh của điểm A qua phép đối xứng trục \(\Delta \).
b) Xác định điểm M thuộc đường thẳng \(\Delta \) sao cho MA + MB đạt giá trị nhỏ nhất.
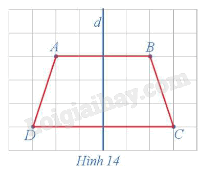
Trong mặt phẳng, cho hình thang cân ABCD, kí hiệu là ℋ. Gọi d là đường thẳng đi qua trung điểm hai cạnh đáy của hình thang cân đó (Hình 14).
Tìm ℋ' = Đd(ℋ).
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(3; 2), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng trục Ox.
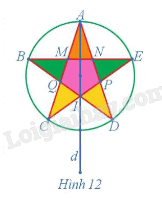
Xác định ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12.
Xét phép đối xứng trục d (Hình 11).
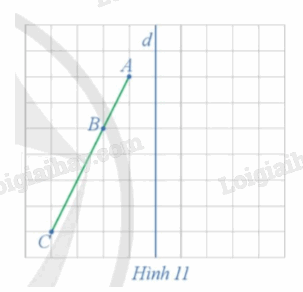
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x1; y1), N(x2; y2). Gọi M', N' lần lượt là ảnh của M và N qua phép đối xứng trục Ox.
a) Xác định tọa độ của hai điểm M' và N'.
b) Viết công thức tính độ dài hai đoạn thẳng MN và M'N', từ đó so sánh hai đoạn thẳng MN và M'N'.
Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC.
Trong mặt phẳng cho đường thẳng d. Với mỗi điểm M trong mặt phẳng và M ∉ d, hãy xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua đường thẳng d) (Hình 9).

Trong mặt phẳng tọa độ Oxy, cho các điểm A(0; 6), B(6; 3) và điểm M thuộc trục hoành.
a) Xác định điểm C đối xứng với B qua trục hoành.
b) Chứng minh rằng MB = MC.
c) Xác định điểm M sao cho tổng MA + MB đạt giá trị nhỏ nhất.
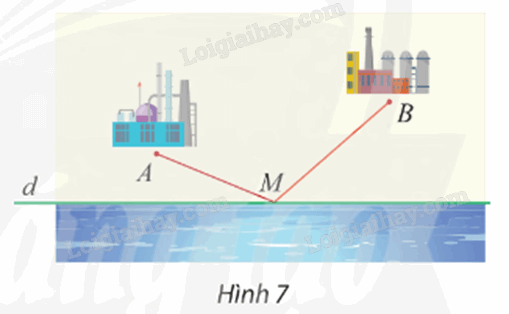
Cho hai điểm A, B là vị trí của hai nhà máy nằm cùng một phía bờ sông là đường thẳng d. Tìm trên bờ sông một địa điểm M để xây dựng một trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ trạm bơm về hai nhà máy là ngắn nhất (Hình 7).
Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(d:{\rm{ }}x-y + 3 = 0\) và đường tròn \(\left( C \right):{\rm{ }}{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2}\; = 9.\)
a) Tìm ảnh của đường thẳng d qua \({Đ_{Oy}}.\)
b) Tìm ảnh của đường tròn (C) qua \({Đ_{Ox}}.\)
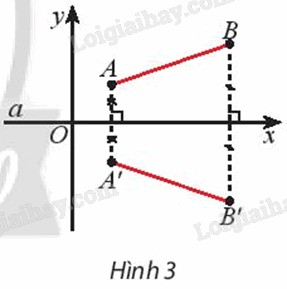
Giả sử Đa là phép đối xứng trục qua đường thẳng a. Ta chọn hệ tọa độ Oxy sao cho trục Ox trùng với a. Lấy hai điểm tùy ý A(xA; yA) và B(xB; yB). Gọi A’, B’ lần lượt là ảnh của A, B qua phép đối xứng trục a (Hình 3). Xác định tọa độ của A’ và B’ rồi dùng công thức tính khoảng cách để so sánh A’B’ và AB.
Tìm trục đối xứng trong các hình ở Hình 10.

Tìm trục đối xứng của một hình thang cân ABCD có hai đáy là AB và CD.
Cho tam giác ABC cân tại A và M là trung điểm của BC. Tìm ảnh của tam giác ABC qua phép đối xứng trục AM.

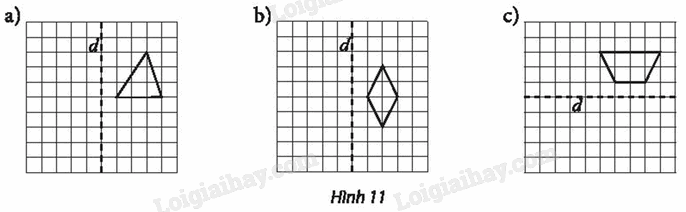
Vẽ các hình sau đây vào giấy kẻ ô vuông và tìm ảnh của các hình đã cho qua phép đối xứng trục d.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình \(x{\rm{ }}-{\rm{ }}y{\rm{ }} = {\rm{ }}0\) và cho điểm \(M({x_0};{\rm{ }}{y_0})\). Tìm tọa độ điểm \(M'{\rm{ }} = {\rm{ }}{Đ_d}\left( M \right)\).
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 2), B(4; –3) và M(–8; 5).
a) Tìm ảnh của A qua \({Đ_{Ox}}\) và ảnh của B qua \({Đ_{Oy}}\).
b) Biết M là ảnh của N qua \({Đ_{Oy}}\). Xác định tọa độ của N.







Danh sách bình luận