Đề bài

Ông An muốn thiết kế một mái che giếng trời hình chóp di động để có thể tùy thích lấy ánh sáng cho ngôi nhà của mình. Biết rằng đáy hình chóp là hình chữ nhật có độ dài hai cạnh đáy là 3 m và 2 m; các cạnh bên bằng nhau (như hình vẽ minh họa). Ông An mong muốn góc giữa mặt phẳng (SBC) và mặt đáy là \(\alpha \) thỏa mãn \({30^o} \le \alpha \le {45^o}\), đồng thời khoảng cách từ điểm A tới mặt phẳng (SBC) là lớn nhất. Tính khoảng cách lớn nhất đó (làm tròn kết quả đến chữ số thập phân thứ hai).

Phương pháp giải

Mô hình hóa mái che thành khối chóp S.ABCD.

Áp dụng quy tắc tính khoảng cách từ điểm đến mặt phẳng, xác định góc giữa hai mặt phẳng trong không gian.

Lời giải của GV Loigiaihay.com

Đáp án :

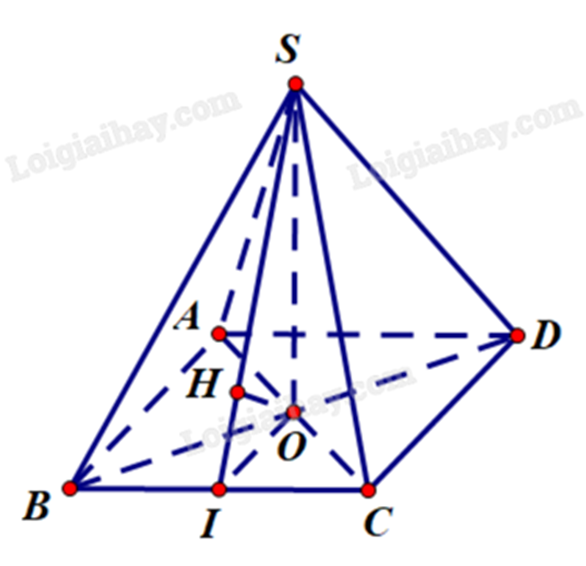
Mô hình hóa mái che thành khối chóp S.ABCD như hình. ABCD là hình chữ nhật, O là giao điểm của AC và BD.

Vì các cạnh bên bằng nhau nên \(SO \bot (ABCD)\).

Gọi I là trung điểm của BC. Khi đó \(SI \bot BC\).

Kẻ \(OH \bot SI\), H thuộc SI.

Ta có \(\left\{ \begin{array}{l}SO \bot (ABCD) \Rightarrow SO \bot BC\\SI \bot BC\end{array} \right. \Rightarrow BC \bot (SOI) \Rightarrow BC \bot OH\).

Mặt khác \(\left\{ \begin{array}{l}OH \bot SI\\OH \bot BC\end{array} \right. \Rightarrow OH \bot (SBC) \Rightarrow d\left( {O,(SBC)} \right) = OH\).

Vì AC = 2OC nên \(d\left( {A,(SBC)} \right) = 2d\left( {O,(SBC)} \right) = 2OH\).

Ông An mong muốn \(d\left( {A,(SBC)} \right)\) max, tức là OH max.

Dễ dàng chứng minh \(\alpha = \left( {(SBC),(ABCD)} \right) = \widehat {SIO}\).

Ta có \({30^o} \le \alpha \le {45^o} \Leftrightarrow \sin {30^o} \le \sin \widehat {SIO} \le \sin {45^o}\)

\( \Leftrightarrow \frac{1}{2} \le \frac{{OH}}{{OI}} \le \frac{{\sqrt 2 }}{2} \Leftrightarrow \frac{{OI}}{2} \le OH \le \frac{{OI\sqrt 2 }}{2}\).

Suy ra OH lớn nhất khi bằng \(\frac{{OI\sqrt 2 }}{2} = \frac{{AB\sqrt 2 }}{4}\).

Mà AB = 2 m hoặc AB = 3 m. Vậy giá trị lớn nhất của OH là \(\frac{{3\sqrt 2 }}{4}\) khi AB = 3.

Vậy giá trị lớn nhất của \(d\left( {A,(SBC)} \right) = 2OH = \frac{{3\sqrt 2 }}{2} \approx 2,12\) (m).

Mở rộng

Các lý thuyết được ứng dụng trong bài:

1. Mô hình hóa hình học:

Biểu diễn một vật thể thực tế (mái che giếng trời) bằng một mô hình toán học (hình chóp).

2. Tính chất của hình chóp có các cạnh bên bằng nhau:

Nếu các cạnh bên của hình chóp bằng nhau, thì hình chiếu vuông góc của đỉnh lên mặt đáy trùng với tâm đường tròn ngoại tiếp đáy.

3. Xác định góc giữa hai mặt phẳng:

Góc giữa hai mặt phẳng cắt nhau là góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng đó và cùng vuông góc với giao tuyến của chúng tại một điểm.

4. Khoảng cách từ một điểm đến một mặt phẳng:

Khoảng cách từ một điểm M đến mặt phẳng (P) là độ dài đoạn thẳng MH, trong đó H là hình chiếu vuông góc của M lên (P). Để tính khoảng cách, ta thường dựng đường thẳng đi qua M vuông góc với (P) và tìm giao điểm H.

5. Hệ thức lượng trong tam giác vuông:

sin (góc) = cạnh đối / cạnh huyền;

cos (góc) = cạnh kề / cạnh huyền;

tan (góc) = cạnh đối / cạnh kề;

cot (góc) = cạnh kề / cạnh huyền.

Báo lỗi/Góp ý

Các bài tập cùng chuyên đề

Bài 1 :

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.

a) Tính độ dài đường chéo của hình lập phương.

b) Chứng minh rằng (ACC′A′) \( \bot \) (BDD′B′).

c) Gọi O là tâm của hình vuông ABCD. Chứng minh rằng \(\widehat {COC'}\) là một góc phẳng của góc nhị diện [C, BD, C']. Tính (gần đúng) số đo của các góc nhị diện [C, BD, C'], [A, BD, C'].