Cho hàm số \((P):y = - \;{x^2}\)
a) Vẽ đồ thị \((P)\) của hàm số trên.
b) Tìm những điểm N thuộc \((P)\) có hoành độ và tung độ là những số đối nhau.
a) Lập bảng giá trị, vẽ đồ thị hàm số trên hệ trục tọa độ.
b) Điểm có hoành độ và tung độ là những số đối nhau có dạng \(N\left( {{x_0}; - {x_0}} \right)\).
Vì \(N \in (P)\) nên \(N\left( {{x_0}; - x_0^2} \right)\).
Do đó \( - {x_0} = - x_0^2\)
Giải phương trình để tìm N thoả mãn.
Ta có bảng giá trị sau:
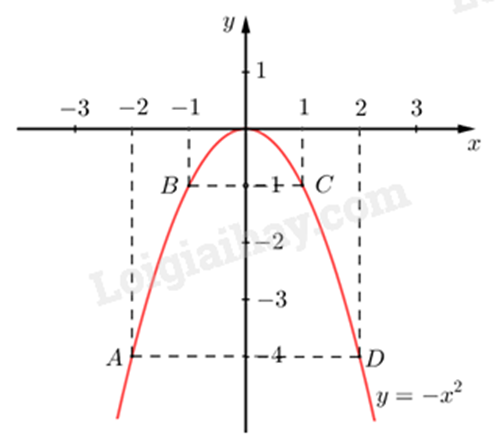
Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 2; - 4} \right);\,\,B\left( { - 1; - 1} \right);C\left( {1; - 1} \right);\,\,D\left( {2; - 4} \right)\)
Hệ số \(a = - 1 < 0\) nên parabol có bề cong hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = - {x^2}\) như sau:
b) Điểm có hoành độ và tung độ là những số đối nhau có dạng \(N\left( {{x_0}; - {x_0}} \right)\).
Vì \(N \in (P)\) nên \(N\left( {{x_0}; - x_0^2} \right)\).
Do đó \( - {x_0} = - x_0^2\)
\(x_0^2 - {x_0} = 0\)
\({x_0}\left( {{x_0} - 1} \right) = 0\)
suy ra \({x_0} = 0\) hoặc \({x_0} - 1 = 0\)
\({x_0} = 0\) hoặc \({x_0} = 1\)
Khi đó \({y_0} = 0\) hoặc \({y_0} = - 1\)
Vậy điểm \(N\) cần tìm là \(N\left( {0;0} \right)\) và \(N\left( {1; - 1} \right)\).
Các bài tập cùng chuyên đề
Xét đồ thị của hàm số \(y = 2{x^2}\) đã vẽ ở HĐ3 (H.6.3).
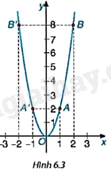
a) Đồ thị nằm về phía trên hay phía dưới trục hoành? Điểm nào là điểm thấp nhất của đồ thị hàm số.
b) So sánh hoành độ và tung độ các cặp điểm thuộc đồ thị: A(1; 2) và \(A'\left( { - 1;2} \right)\); B(2; 8) và \(B'\left( { - 2;8} \right)\).
Từ đó, hãy nhận xét mối liên hệ về vị trí giữa các cặp điểm nêu trên.
c) Tìm điểm C có hoành độ \(x = \frac{1}{2}\) thuộc đồ thị. Xác định tọa độ của điểm C’ đối xứng với điểm C qua trục tung Oy và cho biết điểm C’ có thuộc đồ thị hàm số hay không.
Vẽ đồ thị của hàm số \(y = \frac{1}{2}{x^2}\). Tìm các điểm thuộc đồ thị có tung độ bằng 2 và nhận xét về tính đối xứng giữa các điểm đó.
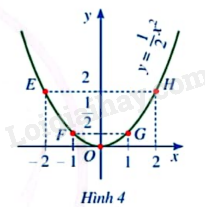
Quan sát đồ thị của hàm số \(y = \frac{1}{2}{x^2}\) ở Hình 4, hãy nêu nhận xét về vị trí cặp điểm E và H, F và G đối với trục Oy.
Cho hàm số \(y = f\left( x \right) = a{x^2}\left( {a \ne 0} \right)\).
a) Chứng tỏ rằng nếu \(\left( {{x_0};{y_0}} \right)\) là một điểm thuộc đồ thị hàm số thì điểm \(\left( { - {x_0};{y_0}} \right)\) cũng nằm trên đồ thị hàm số đó.
b) Chứng minh rằng \(f\left( { - x} \right) = f\left( x \right)\) với mọi x thuộc \(\mathbb{R}\).
Cho điểm \(M\left( {1\,;\, - 5} \right)\) thuộc parabol \(\left( P \right)\) \(y = - 5{x^2}\;\). Tọa độ của N là điểm đối xứng với \(M\)qua trục tung là:
Cho điểm \(M\) có hoành độ \(x = 4\) thuộc parabol \(\left( P \right)\) \(y = \frac{1}{2}{x^2}\). Tọa độ của \(N\) là điểm đối xứng với \(M\) qua trục tung là:
