Cho phép vị tự tâm O, tỉ số k biến điểm M thành điểm M'¸điểm N thành điểm N'.
a) Biểu diễn các vectơ \(\overrightarrow {OM'} ,\,\overrightarrow {ON'} \) tương ứng theo các vectơ \(\overrightarrow {OM} ,\,\overrightarrow {ON} \).
b) Giải thích vì sao \(\overrightarrow {M'N'} = k\overrightarrow {MN} \).
- Dựa và quy tắc hiệu \(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {AB} \).
- Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\).
a) Phép vị tự tâm O, tỉ số k biến điểm M thành điểm M', điểm N thành điểm N' nên ta có \(\overrightarrow {OM'} = k\overrightarrow {OM} \) và \(\overrightarrow {ON'} = k\overrightarrow {ON} \).
b) Ta có: \(\overrightarrow {M'N'} = \overrightarrow {ON'} - \overrightarrow {OM'} = k\overrightarrow {ON} - K\overrightarrow {OM} = k\left( {\overrightarrow {ON} - \overrightarrow {OM} } \right) = k\overrightarrow {MN} \) (theo quy tắc hiệu).
Vậy \(\overrightarrow {M'N'} = k\overrightarrow {MN} \).

Các bài tập cùng chuyên đề
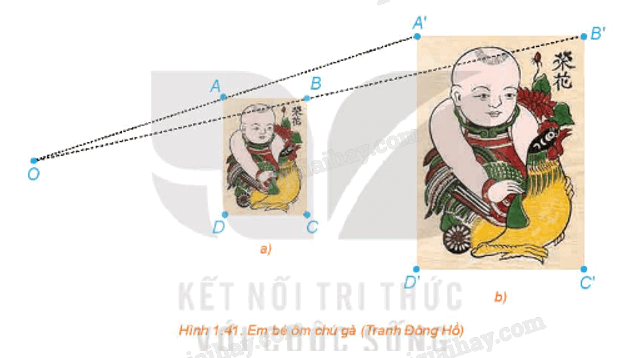
Quan sát hai bức tranh em bé ôm chú gà ở phần mở đầu bài học và chỉ ra phép vị tự biến bức tranh nhỏ thành bức tranh lớn và phép vị tự biến bức tranh lớn thành bức tranh nhỏ.
Chứng minh rằng, phép vị tự \({V_{(O,{\rm{ }}1)}}\) là phép đồng nhất, phép vị tự \({V_{\left( {o,-1} \right)}}\;\) là phép đối xứng tâm O.
Phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm O thành điểm nào? Nếu phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm M thành điểm M' thì phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\) biến điểm M' thành điểm nào?
Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.
a) Giải thích vì sao các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
b) Hãy tính các tỉ số \(\frac{{OA}}{{OA'}},\,\frac{{OB}}{{OB'}},\,\frac{{OC}}{{OC'}},\,\frac{{OD}}{{OD'}}\).
c) Dùng thước thẳng nối hai điểm tương ứng nào đó trên hai bức tranh (chẳng hạn, đầu mỏ trên của chú gà ở hai bức tranh). Đường thẳng đó có đi qua O hay không?
Quan sát Hình 1.47 và cho biết hình nào trong hai hình nhỏ không phải là ảnh của hình lớn qua một phép vị tự. Nêu lí do cho sự lựa chọn đó.

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 1)2 + (y – 2)2 = 25.
a) Tìm tâm I và bán kính R của đường tròn (C).
b) Tìm tâm I' và bán kính R' của đường tròn (C') là ảnh của đường tròn (C) qua phép vị tự tâm A(3; 5), tỉ số 2.
c) Viết phương trình của (C').
Cho hình thang ABCD có hai đáy AB và CD, CD = 2AB. Gọi O là giao của hai cạnh bên và I là giao của hai đường chéo. Tìm ảnh của đoạn thẳng AB qua các phép vị tự V(O, 2), V(I, – 2).
Trong mặt phẳng tọa độ Oxy, cho A(1; 2), B(3; 6). Viết phương trình đường tròn (C) là ảnh của đường tròn đường kính AB qua phép vị tự \({V_{(O,3)}}\).
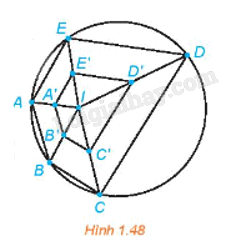
Ở Hình 1.48, A', B', C', D', E' tương ứng là trung điểm của các đoạn thẳng IA, IB, IC, ID, IE. Hỏi năm điểm đó có thuộc một đường tròn hay không? Vì sao?
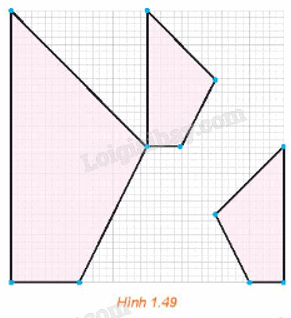
Quan sát ba hình được tô màu ở Hình 1.49, hình nhỏ nào là ảnh của hình lớn qua một phép vị tự?
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 1)2 + (y + 2)2 = 9. Phép vị tự tâm O(0; 0) với tỉ số k = –2 biến đường tròn (C) thành đường tròn (C'). Viết phương trình đường tròn (C').
Cho đường tròn (C) có tâm O bán kính R. Xác định ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số \(k = - \frac{1}{2}\).
Cho phép vị tự tâm O tỉ số k và ba điểm A, B, C thẳng hàng sao cho B nằm giữa A và C. Giả sử \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right),{\rm{ }}C' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( C \right).\)
a) Biểu diễn các vectơ \(\overrightarrow {B'A'} ,\,\overrightarrow {B'C'} \) lần lượt theo các vectơ \(\overrightarrow {BA} ,\,\overrightarrow {BC} \).
b) Hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \) có ngược hướng không?
c) Hai vectơ \(\overrightarrow {B'A'} \) và \(\overrightarrow {B'C'} \) có ngược hướng không? Từ đó, nêu mối quan hệ giữa ba điểm A', B', C'.
Cho phép vị tự tâm O tỉ số k và hai điểm A, B. Giả sử \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right).\)
a) Biểu diễn các vectơ \(\overrightarrow {OA'} ,\,\overrightarrow {OB'} \) lần lượt theo các vectơ \(\overrightarrow {OA} ,\,\overrightarrow {OB} \).
b) Biểu diễn các vectơ \(\overrightarrow {A'B'} \) theo vectơ \(\overrightarrow {AB} \). Từ đó, tìm mối liên hệ độ dài giữa hai đoạn thẳng A'B' và AB.
Cho tam giác ABC có O là trung điểm của cạnh BC. Xác định ảnh của tam giác ABC trong phép vị tự tâm O tỉ số \(k = \frac{1}{2}\).
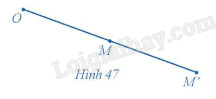
Trong mặt phẳng cho điểm O. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho \(\overrightarrow {OM'} = 2\overrightarrow {OM} \) (Hình 47).
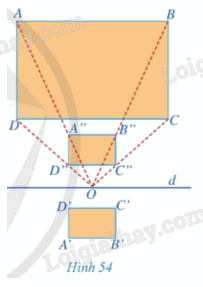
Quan sát Hình 54 và cho biết:
a) Hình chữ nhật A"B"C"D" nhận được từ hình chữ nhật ABCD bằng cách nào.
b) Hình chữ nhật A'B'C'D' nhận được từ hình chữ nhật A"B"C"D" bằng cách nào.
c) Phép đồng dạng nào biến hình chữ nhật ABCD thành hình chữ nhật A'B'C'D'.
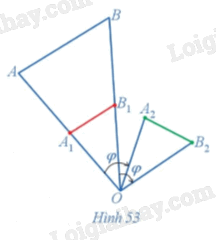
Trong Hình 53, cho đoạn thẳng AB. Nêu cách dựng:
a) Đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép vị tự tâm O tỉ số \(\frac{1}{2}\);
b) Đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép quay tâm O với góc quay \(\varphi = -60^\circ .\)
c) Nhận xét về mối liên hệ giữa độ dài các đoạn thẳng \(AB,{\rm{ }}{A_2}{B_2}.\)
Phép biến hình nào trong các phép biến hình dưới đây là phép vị tự?
a) Phép tịnh tiến theo vectơ khác \(\vec 0\);
b) Phép đối xứng tâm;
c) Phép đối xứng trục;
d) Phép quay.
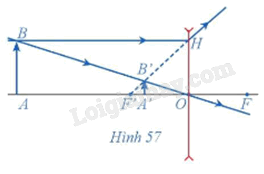
Một thấu kính phân kì có tiêu cự OF = OF' = 20 cm (kính cận). Vật sáng AB được đặt vuông góc với trục chính của thấu kính, cách thấu kính một đoạn OA = 60 cm, qua thấu kính cho ảnh ảo A'B' (Hình 57). A'B' là ảnh của AB qua một phép vị tự tâm O tỉ số k.
Tính khoảng cách A'O từ ảnh đến thấu kính và so sánh khoảng cách đó với khoảng cách AO từ vật đến thấu kính.
Chứng minh rằng qua phép vị tự tâm O tỉ số k (k ≠ 0), ảnh của mọi đường thẳng đi qua tâm O là chính nó.
Cho tam giác nhọn ABC có trực tâm H. Xác định ảnh của tam giác ABC qua phép vị tự tâm H tỉ số \(k = \frac{1}{2}\).
Cho hai đường tròn (O1; R) và (O2; 2R) tiếp xúc ngoài với nhau tại điểm A. Tìm phép vị tự biến đường tròn (O1; R) thành đường tròn \(({O_2};{\rm{ }}2R)\).
Trong sách báo, tranh ảnh hay trong thực tế có những hình ảnh với hình dạng hoàn toàn giống nhau, chỉ khác nhau về kích thước. Những hình như vậy có liên quan gì về mặt hình học và phép biến hình nào đã tạo ra hình này từ hình kia?

Thước vẽ truyền là một dụng cụ gồm bốn thanh gỗ hoặc kim loại được ghép với nhau nhờ bốn khớp xoay tại các điểm A, B, C, D sao cho ABCD là hình bình hành và ba điểm O, D, D’ thẳng hàng. Khi sử dụng, người vẽ ghim cố định điểm O xuống mặt giấy (thước vẫn có thể xoay quanh O). Đặt hai cây bút tại hai điểm D và D’. Khi đầu bút D vẽ hình ℋ, đầu bút D’ sẽ tự động vẽ truyền cho ta hình ℋ ’ là ảnh của ℋ.

a) Xác định tâm và tỉ số k của phép vị tự được sử dụng trong cây thước vẽ truyền ở Hình 5.
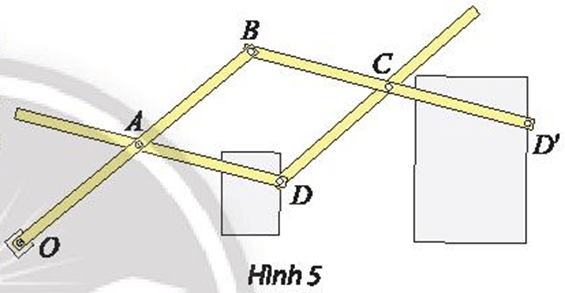
b) Nếu ngược lại cho đầu bút D’ vẽ hình ℋ ’ khi đó đầu bút D sẽ tự động vẽ truyền cho ta hình ℋ là ảnh của ℋ ’. Xác định phép vị tự trong trường hợp này.
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; 9). Tìm tọa độ các điểm M1 và M2 lần lượt là ảnh của M qua các phép vị tự \({V_{\left( {O,{\rm{ }}3} \right)}}\;\) và \({V_{(O,{\rm{ }}-2)}}\).
Trong Hình 1, cho biết A’, B’, C’ lần lượt là trung điểm của OA, OB, OC.
a) Xét xem hai tam giác ABC và A’B’C’ đồng dạng không?
b) Thảo luận nhóm để tìm xem có phép biến hình nào biến tam giác ABC thành tam giác A’B’C’ không?

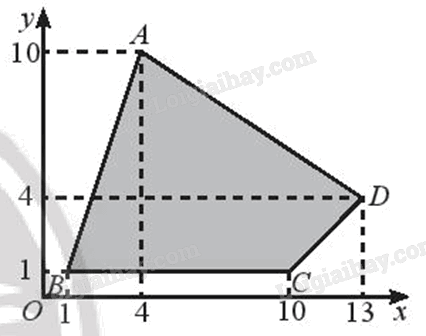
Vẽ Hình 11 ra giấy kẻ ô li và tìm ảnh của tứ giác ABCD qua phép vị tự \({V_{\left( {O, - \frac{1}{2}} \right)}}\).
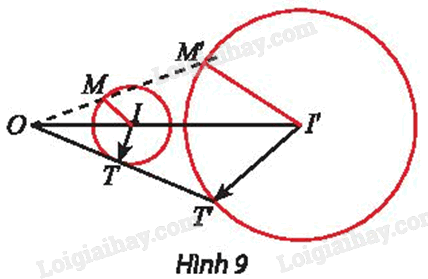
Cho phép vị tự \({V_{\left( {O,{\rm{ }}k} \right)}}\) và đường tròn (C) tâm I bán kính r. Xét điểm M thuộc (C), gọi I’ và M’ là ảnh của I và M qua phép vị tự \({V_{\left( {O,{\rm{ }}k} \right)}}.\)
a) Tính I’M’ theo r và k.
b) Khi cho điểm M chạy trên đường tròn (C) thì M’ chạy trên đường nào?
Cho tam giác ABC có G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác. Gọi A’, B’, C’ lần lượt là trung điểm các cạnh BC, CA, AB.
a) Tìm phép vị tự biến tam giác ABC thành tam giác A’B’C’.
b) Chứng minh ba điểm H, G, O thẳng hàng.







Danh sách bình luận