Côsin của góc giữa hai vectơ \(\overrightarrow u = (1;1)\) và \(\overrightarrow v = ( - 2;1)\) là:
A. \( - \frac{1}{{10}}\)
B. \(\frac{{\sqrt {10} }}{{10}}\)
C. \( - \frac{{\sqrt {10} }}{{10}}\)
D. \(\frac{3}{{10}}\)
Sử dụng công thức tính cos \(\left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{{x_1}.{x_2} + {y_1}.{y_2}}}{{\sqrt {x_1^2 + y_1^2} .\sqrt {x_2^2 + y_2^2} }}\) với \(\overrightarrow u ({x_1};{y_1}),\overrightarrow v ({x_2};{y_2})\).
Ta có: \(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{1.( - 2) + 1.1}}{{\sqrt {{1^2} + {1^2}} .\sqrt {{{( - 2)}^2} + {1^2}} }}\)\( = - \frac{{\sqrt {10} }}{{10}}\).
Chọn C
Các bài tập cùng chuyên đề
Cho tam giác đều ABC. Tính \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\).
Khi nào thì góc giữa hai vectơ bằng \({0^o}\), bằng \({180^o}?\)
Trong hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \). Hãy tìm số đo các góc giữa \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \), \(\overrightarrow {DA} \) và \(\overrightarrow {DB} \).
Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) trong mỗi trường hợp sau:
a) \(\overrightarrow a = ( - 3;1),\;\overrightarrow b = (2;6)\)
b) \(\overrightarrow a = (3;1),\;\overrightarrow b = (2;4)\)
c) \(\overrightarrow a = ( - \sqrt 2 ;1),\;\overrightarrow b = (2; - \sqrt 2 )\)
Tìm điều kiện của \(\overrightarrow u ,\;\overrightarrow v \) để:
a) \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|\)
b) \(\overrightarrow u .\;\overrightarrow v = - \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|\)
Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc:
\(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right),\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right)\).
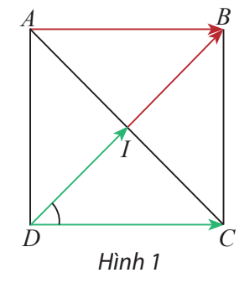
Cho hình vuông ABCD có tâm I (Hình 1).
a) Tính \(\widehat {IDC}\).
b) Tìm hai vectơ cùng có điểm đầu là D và điểm cuối lần lượt là I và C
c) Tìm hai vectơ có điểm đầu là D và lần lượt bằng vectơ \(\overrightarrow {IB} \)và \(\overrightarrow {AB} \)
Cho hai vectơ có độ dài lần lượt là 6 và 8 và có tích vô hướng là 24. Tính góc giữa hai vectơ đó.
Tam giác ABC vuông ở A và có \(\widehat B = 50^\circ \). Khẳng định nào sau đây là sai?
A. \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = 130^\circ \)
B. \(\left( {\overrightarrow {BC} ,\overrightarrow {AC} } \right) = 40^\circ \)
C. \(\left( {\overrightarrow {AB} ,\overrightarrow {CB} } \right) = 50^\circ \)
D. \(\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = 120^\circ \)
Tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)trong các trường hợp sau:
a) \(\overrightarrow a = (2; - 3),\overrightarrow b = (6;4)\).
b) \(\overrightarrow a = (3;2),\overrightarrow b = (5; - 1)\).
c) \(\overrightarrow a = ( - 2; - 2\sqrt 3 ),\overrightarrow b = (3;\sqrt 3 )\).
Cho hai đường thẳng
\({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) (\({a_1}^2 + {b_1}^2 > 0\)) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) \(\left( {{a_2}^2 + {b_2}^2 > 0} \right)\)
có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
Tìm tọa độ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \)và tính \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\).
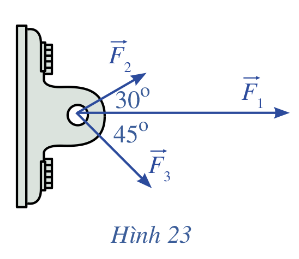
Một vật đồng thời bị ba lực tác động: lực tác động thứ nhất \(\overrightarrow {{F_1}} \) có độ lớn là 1 500 N, lực tác động thứ hai\(\overrightarrow {{F_2}} \) , có độ lớn là 600 N, lực tác động thứ ba\(\overrightarrow {{F_3}} \) , có độ lớn là 800 N. Các lực này được biểu diễn bằng những vectơ như Hình 23, với \(\left( {\overrightarrow {{F_1}} ,{\rm{ }}\overrightarrow {{F_2}} } \right)\) = 30°, \(\left( {\overrightarrow {{F_1}} ,{\rm{ }}\overrightarrow {{F_3}} } \right)\)= 45° và \(\left( {\overrightarrow {{F_2}} ,{\rm{ }}\overrightarrow {{F_3}} } \right)\) = 75°. Tính độ lớn lực tổng hợp tác động lên vật (làm tròn kết quả đến hàng đơn vị).
Cho tam giác ABC đều. Tính góc \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\).
Tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) trong các trường hợp sau:
a) \(\overrightarrow a = \left( {1; - 4} \right),\overrightarrow b = \left( {5;3} \right)\).
b) \(\overrightarrow a = \left( {4;3} \right),\overrightarrow b = \left( {6;0} \right)\).
c) \(\overrightarrow a = \left( {2;2\sqrt 3 } \right),\overrightarrow b = \left( { - 3;\sqrt 3 } \right)\).
Cho hai vectơ \(\overrightarrow a = \left( {4;3} \right)\) và \(\overrightarrow b = \left( {1;7} \right)\). Góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là:
A. \({90^ \circ }\)
B. \({60^ \circ }\)
C. \({45^ \circ }\)
D. \({30^ \circ }\)
Cho hai vectơ \(\overrightarrow u = ( - 4; - 3)\) và \(\overrightarrow v = ( - 1; - 7)\). Góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là:
A. 90⁰
B. 60⁰
C. 45⁰
D. 30⁰
