Gương phản chiếu của một đèn pha có mặt cắt là một parabol (P) với tim bóng đèn đặt ở tiêu điểm F. Chiều rộng giữa hai mép gương là 50 cm, chiều sâu của gương là 40 cm. Viết phương trình chính tắc của (P).
Parabol \(\left( P \right)\) có dạng \({y^2} = 2px\) với \(p > 0\) có tiêu điểm \(F\left( {\frac{p}{2};0} \right)\), phương trình đường chuẩn \(\Delta :x = - \frac{p}{2}\).
Gọi phương trình \(\left( P \right)\) có dạng \({y^2} = 2px\).
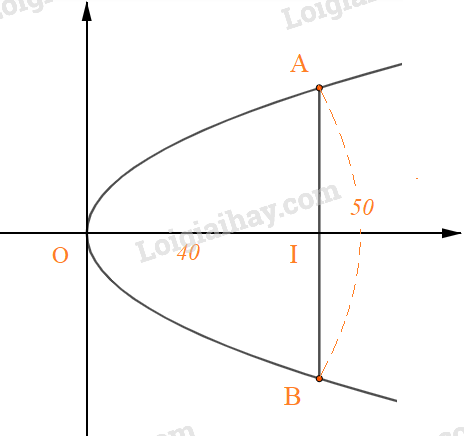
Khi đó gương là phần mặt phẳng tạo bởi đường cong AOB.
Ta có: Chiều rộng giữa hai mép gương là 50 cm, suy ra AB = 50cm.
Chiều sâu của gương là 40 cm suy ra OI = 40 cm.
Do đó AI = 50: 2= 25 và A(40; 25) thuộc vào parabol (P).
Thay điểm \(A\left( {40;25} \right)\) vào phương trình ta có \(p = \frac{{{y^2}}}{{2x}} = \frac{{{{25}^2}}}{{2.40}} \approx 7,8\).
\( \Rightarrow \left( P \right):{y^2} = 15,6x\).

Các bài tập cùng chuyên đề
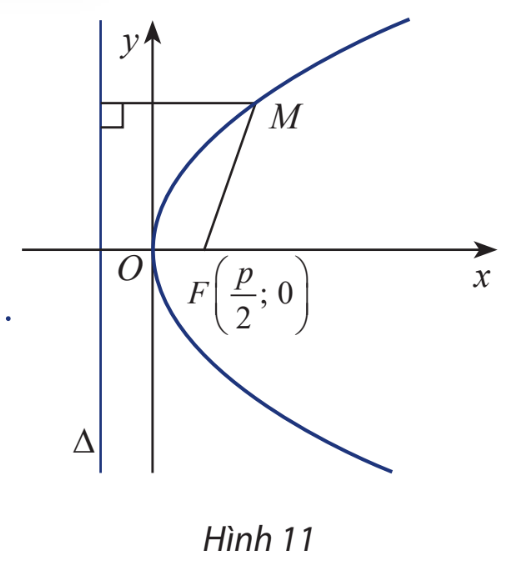
Xét (P) là một parabol với tiêu điểm F và đường chuẩn \(\Delta \). Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên \(\Delta \). Chọn hệ trục toạ độ Oxy Có gốc O là trung điểm của HF, tia Ox trùng tia OF (H7.27).
a) Nêu toạ độ của F và phương trình của \(\Delta \).
b) Giải thích vì sao điềm M(x; y) thuộc (P) khi và chỉ khi \(\sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\).
Lập phương trình chính tắc của parabol đi qua điểm \(M\left( {2;4} \right)\).
Phương trình nào sau đây là phương trình chính tắc của đường parabol?
A. \({x^2} = 4y\)
B. \({x^2} = - 6y\)
C. \({y^2} = 4x\)
D. \({y^2} = - 4x\)
Viết phương trình chính tắc của parabol (P) có đường chuẩn \(\Delta :x + 1 = 0\).
Cho parabol (P) có tiêu điểm F và đường chuẩn \(\Delta \). Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên \(p > 0\).
Chọn hệ trục tọa độ Oxy sao cho \(F\left( {\frac{p}{2};0} \right)\) và \(\Delta :x + \frac{p}{2} = 0\).
Xét điểm \(M(x;y)\).
a) Tính MF và \(d\left( {M,\Delta } \right)\).
b) Giải thích biểu thức sau:
\(M(x;y) \in (P) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\).
Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:
a) \({y^2} = 12x\)
b) \({y^2} = x\)
Viết phương trình chính tắc của parabol thỏa mãn từng điều kiện sau:
a) Tiêu điểm \((4;0)\)
b) Đường chuẩn có phương trình \(x = - \frac{1}{6}\)
c) Đi qua điểm \((1;4)\)
d) Khoảng cách từ tiêu điểm đến đường chuẩn bằng 8
Viết phương trình các parabol sau đây dưới dạng chính tắc:
a) \(x = \frac{{{y^2}}}{4}\)
b) \(x-y^2=0\)
Những phương trình nào sau đây là phương trình chính tắc của parabol?
a) \({y^2} = - 2x\)
b) \({y^2} = 2x\)
c) \({x^2} = - 2y\)
d) \({y^2} = \sqrt 5 x\)
Tìm tọa độ tiêu điểm và viết phương trình đường chuẩn của đường parabol trong mỗi trường hợp sau:
a) \({y^2} = \frac{{5x}}{2}\)
b) \({y^2} = 2\sqrt 2 x\)
Viết phương trình chính tắc của đường parabol, biết tiêu điểm \(F\left( {6;0} \right)\).
Một chiếc đèn có mặt cắt ngang là hình parabol (Hình 63). Hình parabol có chiều rộng giữa hai mép vành là AB = 40 cm và chiều sâu h = 30 cm (h bằng khoảng cách từ O đến AB). Bóng đèn nằm ở tiêu điểm S. Viết phương trình chính tắc của parabol đó.
Cho parabol \(\left( P \right)\) có phương trình \({y^2} = 4x\). Tìm tiêu điểm và đường chuẩn của parabol.
Viết phương trình chính tắc của parabol \(\left( P \right)\), biết rằng \(\left( P \right)\) có đường chuẩn là đường thẳng \(\Delta :x + 4 = 0\). Tìm tọa độ điểm M thuộc \(\left( P \right)\) sao cho khoảng cách từ M đến tiêu điểm của \(\left( P \right)\) bằng 5.
Cho parabol \(\left( P \right)\) có phương trình \({y^2} = 16x\). Gọi \(\Delta \) là đường thẳng bất kì đi qua tiêu điểm F của \(\left( P \right)\) và không trùng với trục hoành. Chứng minh rằng \(\Delta \) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt A, B, đồng thời tích các khoảng cách từ A và B đến trục hoành không đổi.
Phương trình chính tắc của parabol \(\left( P \right)\) đi qua điểm \(E\left( {2;2} \right)\) là:
A. \({x^2} = 2y\)
B. \({x^2} = 4y\)
C. \({x^2} = y\)
D. \(y = 2{x^2}\)
Lập phương trình chính tắc của parabol \(\left( P \right)\), biết rằng \(\left( P \right)\) đi qua điểm \(A\left( {2;4} \right)\). Khi đó hãy tìm điểm M thuộc \(\left( P \right)\) và cách tiêu điểm của \(\left( P \right)\) một khoảng bằng 5.
Phương trình chính tắc của parabol có tiêu điểm \(\left( {2;0} \right)\) là:
A. \({y^2} = 8x\)
B. \({y^2} = 4x\)
C. \({y^2} = 2x\)
D. \(y = 2{x^2}\)
Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:
a) \({y^2} = 4x\).
b) \({y^2} = 2x\).
c) \({y^2} = - 6x\).
Viết phương trình chính tắc của parabol thỏa mãn các điều kiện:
a) Tiêu điểm \(\left( {8;0} \right)\).
b) Khoảng cách từ tiêu điểm đến đường chuẩn bằng 4.
Parabol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng:
\({y^2} = 2px\) (p > 0)?
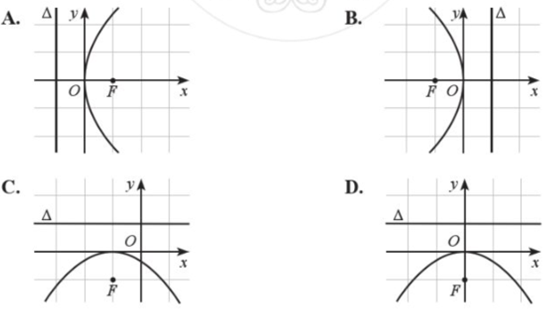
Viết phương trình chính tắc của parabol (P), biết:
a) Phương trình đường chuẩn của (P) là \(x + \frac{1}{8} = 0\).
b) (P) đi qua điểm M(1 ; -8).
Cho parabol (P) có phương trình chính tắc: y2 = 2px (p > 0) và đường thẳng x = m (m > 0) cắt (P) tại hai điểm I, K phân biệt. Chứng minh hai điểm I và K đối xứng nhau qua trục Ox.
Phương trình nào dưới đây là phương trình chính tắc của đường parabol?
A. \({y^2} = \frac{x}{{10}}\)
B. \({y^2} = \frac{{ - x}}{{10}}\)
C. \({x^2} = \frac{y}{{10}}\)
D. \({x^2} = \frac{{ - y}}{{10}}\)







Danh sách bình luận