Viết phương trình chính tắc của đường parabol, biết tiêu điểm \(F\left( {6;0} \right)\).
Phương trình chính tắc của parabol là: \({y^2} = 2px\left( {p > 0} \right)\), trong đó tiêu điểm là \(F\left( {\frac{p}{2};0} \right)\) và phương trình đường chuẩn là: \(x + \frac{p}{2} = 0\).
Do parabol có tiêu điểm là \(F\left( {6;0} \right)\) nên ta có \(\frac{p}{2} = 6 \Leftrightarrow p = 12\).
Vậy phương trình chính tắc của parabol là: \({y^2} = 24x\).

Các bài tập cùng chuyên đề
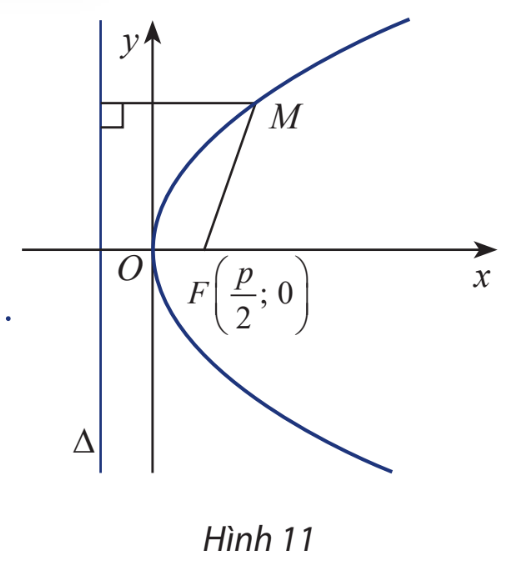
Xét (P) là một parabol với tiêu điểm F và đường chuẩn \(\Delta \). Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên \(\Delta \). Chọn hệ trục toạ độ Oxy Có gốc O là trung điểm của HF, tia Ox trùng tia OF (H7.27).
a) Nêu toạ độ của F và phương trình của \(\Delta \).
b) Giải thích vì sao điềm M(x; y) thuộc (P) khi và chỉ khi \(\sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\).
Lập phương trình chính tắc của parabol đi qua điểm \(M\left( {2;4} \right)\).
Phương trình nào sau đây là phương trình chính tắc của đường parabol?
A. \({x^2} = 4y\)
B. \({x^2} = - 6y\)
C. \({y^2} = 4x\)
D. \({y^2} = - 4x\)
Viết phương trình chính tắc của parabol (P) có đường chuẩn \(\Delta :x + 1 = 0\).
Cho parabol (P) có tiêu điểm F và đường chuẩn \(\Delta \). Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên \(p > 0\).
Chọn hệ trục tọa độ Oxy sao cho \(F\left( {\frac{p}{2};0} \right)\) và \(\Delta :x + \frac{p}{2} = 0\).
Xét điểm \(M(x;y)\).
a) Tính MF và \(d\left( {M,\Delta } \right)\).
b) Giải thích biểu thức sau:
\(M(x;y) \in (P) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\).
Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:
a) \({y^2} = 12x\)
b) \({y^2} = x\)
Viết phương trình chính tắc của parabol thỏa mãn từng điều kiện sau:
a) Tiêu điểm \((4;0)\)
b) Đường chuẩn có phương trình \(x = - \frac{1}{6}\)
c) Đi qua điểm \((1;4)\)
d) Khoảng cách từ tiêu điểm đến đường chuẩn bằng 8
Viết phương trình các parabol sau đây dưới dạng chính tắc:
a) \(x = \frac{{{y^2}}}{4}\)
b) \(x-y^2=0\)
Những phương trình nào sau đây là phương trình chính tắc của parabol?
a) \({y^2} = - 2x\)
b) \({y^2} = 2x\)
c) \({x^2} = - 2y\)
d) \({y^2} = \sqrt 5 x\)
Tìm tọa độ tiêu điểm và viết phương trình đường chuẩn của đường parabol trong mỗi trường hợp sau:
a) \({y^2} = \frac{{5x}}{2}\)
b) \({y^2} = 2\sqrt 2 x\)
Một chiếc đèn có mặt cắt ngang là hình parabol (Hình 63). Hình parabol có chiều rộng giữa hai mép vành là AB = 40 cm và chiều sâu h = 30 cm (h bằng khoảng cách từ O đến AB). Bóng đèn nằm ở tiêu điểm S. Viết phương trình chính tắc của parabol đó.
Cho parabol \(\left( P \right)\) có phương trình \({y^2} = 4x\). Tìm tiêu điểm và đường chuẩn của parabol.
Viết phương trình chính tắc của parabol \(\left( P \right)\), biết rằng \(\left( P \right)\) có đường chuẩn là đường thẳng \(\Delta :x + 4 = 0\). Tìm tọa độ điểm M thuộc \(\left( P \right)\) sao cho khoảng cách từ M đến tiêu điểm của \(\left( P \right)\) bằng 5.
Cho parabol \(\left( P \right)\) có phương trình \({y^2} = 16x\). Gọi \(\Delta \) là đường thẳng bất kì đi qua tiêu điểm F của \(\left( P \right)\) và không trùng với trục hoành. Chứng minh rằng \(\Delta \) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt A, B, đồng thời tích các khoảng cách từ A và B đến trục hoành không đổi.
Phương trình chính tắc của parabol \(\left( P \right)\) đi qua điểm \(E\left( {2;2} \right)\) là:
A. \({x^2} = 2y\)
B. \({x^2} = 4y\)
C. \({x^2} = y\)
D. \(y = 2{x^2}\)
Lập phương trình chính tắc của parabol \(\left( P \right)\), biết rằng \(\left( P \right)\) đi qua điểm \(A\left( {2;4} \right)\). Khi đó hãy tìm điểm M thuộc \(\left( P \right)\) và cách tiêu điểm của \(\left( P \right)\) một khoảng bằng 5.
Phương trình chính tắc của parabol có tiêu điểm \(\left( {2;0} \right)\) là:
A. \({y^2} = 8x\)
B. \({y^2} = 4x\)
C. \({y^2} = 2x\)
D. \(y = 2{x^2}\)
Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:
a) \({y^2} = 4x\).
b) \({y^2} = 2x\).
c) \({y^2} = - 6x\).
Viết phương trình chính tắc của parabol thỏa mãn các điều kiện:
a) Tiêu điểm \(\left( {8;0} \right)\).
b) Khoảng cách từ tiêu điểm đến đường chuẩn bằng 4.
Gương phản chiếu của một đèn pha có mặt cắt là một parabol (P) với tim bóng đèn đặt ở tiêu điểm F. Chiều rộng giữa hai mép gương là 50 cm, chiều sâu của gương là 40 cm. Viết phương trình chính tắc của (P).
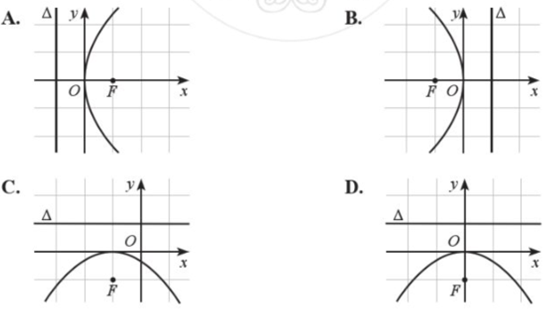
Parabol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng:
\({y^2} = 2px\) (p > 0)?
Viết phương trình chính tắc của parabol (P), biết:
a) Phương trình đường chuẩn của (P) là \(x + \frac{1}{8} = 0\).
b) (P) đi qua điểm M(1 ; -8).
Cho parabol (P) có phương trình chính tắc: y2 = 2px (p > 0) và đường thẳng x = m (m > 0) cắt (P) tại hai điểm I, K phân biệt. Chứng minh hai điểm I và K đối xứng nhau qua trục Ox.
Phương trình nào dưới đây là phương trình chính tắc của đường parabol?
A. \({y^2} = \frac{x}{{10}}\)
B. \({y^2} = \frac{{ - x}}{{10}}\)
C. \({x^2} = \frac{y}{{10}}\)
D. \({x^2} = \frac{{ - y}}{{10}}\)







Danh sách bình luận