Cho hypebol \(\left( H \right)\) có phương trình \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{{20}} = 1\). Tìm tiêu điểm và tiêu cự của hypebol.

Cho (H): \(\frac{{{x^2}}}{{144}} - \frac{{{y^2}}}{{25}} = 1\). Tìm các tiêu điểm và tiêu cự của (H).

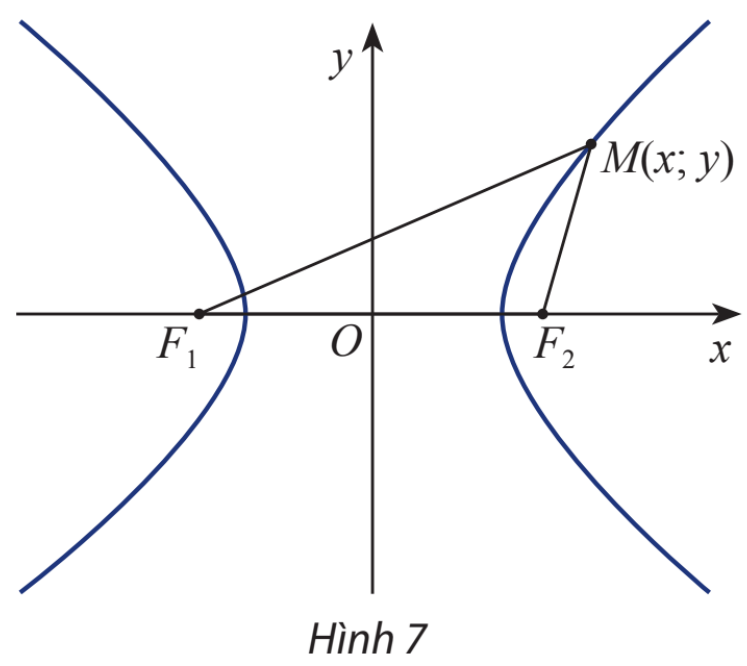
Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm của \({F_1}{F_2}\), tia Ox trùng tia\(O{F_2}\) , (H.7.26). Nêu toạ độ của các tiêu điềm \({F_1},{F_2}\). Giải thích vì sao điểm M(x; y) thuộc (H) khi và chỉ khi \(\left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}}  - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\).

Cho hình chữ nhật ABCD và M, N tương ứng là trung điểm của các cạnh AB, CD (H725). Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N.

Tại sao trong định nghĩa hypebol cần điều kiện a < c?

Cho hyperbol có phương trình \(\frac{{{x^2}}}{7} - \frac{{{y^2}}}{9} = 1\). Tìm tiêu điểm và tiêu cự của hyperbol.

Phương trình nào sau đây là phương trình chính tắc của đường hyperbol?

A. \(\frac{{{x^2}}}{3} - \frac{{{y^2}}}{2} =  - 1\)

B. \(\frac{{{x^2}}}{1} - \frac{{{y^2}}}{6} = 1\)

C. \(\frac{{{x^2}}}{6} + \frac{{{y^2}}}{1} = 1\)

D. \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{1} =  - 1\)

Cho hypebol có phương trình: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)

 a) Tìm các giao điểm \({A_1},{A_2}\)của hypebol với trục hoành (hoành độ của \({A_1}\)nhỏ hơn của \({A_2}\)).

b) Chứng minh rằng, nếu điểm M(x; y) thuộc nhánh nằm bên trái trục tung của hypebol thì \(x \le  - a\) , nêu điêm M(x, y) thuộc nhánh nằm bên phải trực tung của hypebol thì \(x \ge a\).

c) Tìm các điểm\({M_1},{M_2}\) tương ứng thuộc các nhánh bên trái, bên phải trực tung của hypebol để \({M_1}{M_2}\) nhỏ nhất.

Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục nhỏ bằng 6.

Cho hyperbol  (H) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt điểm \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( - c;0)\) và \({F_2}(c;0)\).

Xét điểm \(M(x;y)\).

a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c.

b) Giải thích phát biểu sau:

\(M(x;y) \in (H) \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}}  - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\).

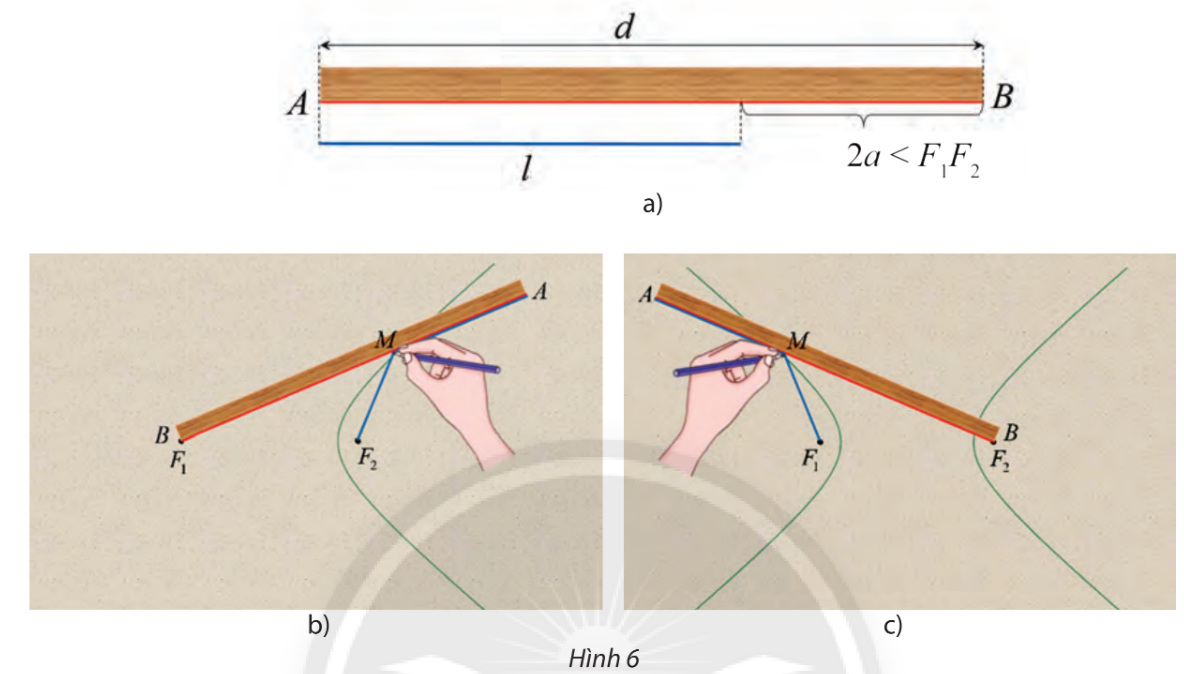
Lấy một tấm bìa, trên đó đánh dấu hai điểm \({F_1}\) và \({F_2}\). Lấy một cây thước thẳng với mép thước  AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài l sao cho \(d - l = 2a\) nhỏ hơn khoảng cách \({F_1}{F_2}\) (hình 6a).

Đính một đầu dây vào đầu A của thước, dùng đinh ghim đầu dây còn lại vào điểm \({F_2}\). Đặt thước sao cho đầu B của thước trùng với điểm \({F_1}\). Tựa đầu bút chì vào dây, di chuyển điểm M trên tấm bìa và giữ sao cho dây luôn căng, đoạn AM ép sát vào thước, khi đó M sẽ gạch lên tấm bìa một đường (H) (xem hình 6b).

a) Chứng tỏ rằng khi M di động, ta luôn có \(M{F_1} - M{F_2} = 2a\).

b) Vẫn đính một đầu dây vào đầu A của thước nhưng đổi chỗ cố định đầu dây còn lại vào \({F_1}\), đầu B của thước trùng với \({F_2}\) sao cho đoạn thẳng BA có thể quay quanh \({F_2}\)và làm tương tự như lần đầu để bút chì M vẽ được một nhánh khác của đường (H) (hình 6c). Tính \(M{F_2} - M{F_1}\).

Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo của các hypebol sau:

a) \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)

b)  \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)

c) \({x^2} - 16{y^2} = 16\)

d) \(9{x^2} - 16{y^2} = 144\)

Viết phương trình chính tắc của hypebol thỏa mãn từng điều kiện sau:

a) Đỉnh \((3;0)\), tiêu điểm \((5;0)\)

b) Độ dài trục thực 8, độ dài trục ảo 6

Viết phương trình hypebol sau đây dưới dạng chính tắc: \(4{x^2}-9{y^2} = {\rm{ }}1.\)

Đóng hai chiếc đinh cố định tại hai điểm \({F_1},{F_2}\) trên mặt một bảng gỗ. Lấy một thước thẳng có mép AB và một sợi dây không đàn hồi có chiều dài \(l\)  thoả mãn\(AB-{F_1}{F_2}{\rm{ }} < l < AB\) . Đính một đầu dây vào điểm A và đầu dây kia vào \({F_2}\). Đặt thước sao cho điểm B trùng với \({F_1}\), và lấy đầu bút chì (kí hiệu là M) tì sát sợi dây vào thước thẳng sao cho sợi dây luôn bị căng. Sợi dây khi đó là đường gấp khúc\(AM{F_2}\) , Cho thước quay quanh điểm B (trùng \({F_1}\)), tức là điểm A chuyển động trên đường tròn tâm B có bán kính bằng độ dài đoạn thẳng AB, mép thước luôn áp sát mặt gỗ (Hình 53). Khi đó, đầu bút chì M sẽ vạch nên một đường mà ta gọi là đường hypebol. Khi M thay đổi, có nhận xét gì về hiệu\(M{F_1} - M{F_2}\)?

Những phương trình nào sau đây là phương trình chính tắc của hypebol?

a) \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{9} = 1\)

b) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{9} = 1\)

c) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{64}} = 1\)

d) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{9} = 1\)

Tìm tọa độ các tiêu điểm của đường hypebol trong mỗi trường hợp sau:

a) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\)

b) \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{25}} = 1\)

Viết phương trình chính tắc của hypebol \(\left( H \right)\), biết \(N\left( {\sqrt {10} ;2} \right)\) nằm trên \(\left( H \right)\) và hoành độ một giao điểm của \(\left( H \right)\) với trục Ox bằng 3.

Viết phương trình chính tắc của hypebol \(\left( H \right)\), biết \(\left( H \right)\) đi qua điểm \(M\left( {3\sqrt 2 ; - 4} \right)\) và có một tiêu điểm \({F_2}\left( {5;0} \right)\).

Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường hypebol?

A. \(16{x^2} - 5{y^2} =  - 80\)

B. \({x^2} = 4y\)

C. \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{1} = 1\)

D. \(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{1} = 1\)

Cho hypebol \(\left( H \right)\) có phương trình chính tắc \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{13}} = 1\). Tiêu cự của hypebol là:

A. 7  

B. 14

C. \(2\sqrt {23} \) 

D. \(\sqrt {23} \)

Phương trình chính tắc của hypebol có hai đỉnh \(\left( { - 4;0} \right),\left( {4;0} \right)\) và hai tiêu điểm là \(\left( { - 5;0} \right),\left( {5;0} \right)\) là:

A. \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{{25}} = 1\)    

B. \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)  

C. \(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{9} = 1\)

D. \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\)

Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo các hypebol sau:

a) \(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{{144}} = 1\).   

b) \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\).

Viết phương trình chính tắc của hypebol thỏa mãn các điều kiện sau:

a) Đỉnh \(\left( { - 6;0} \right)\) và \(\left( {6;0} \right)\); tiêu điểm \(\left( { - 10;0} \right)\) và \(\left( {10;0} \right)\).

b) Độ dài trục thực là 10, độ dài trục ảo là 20.

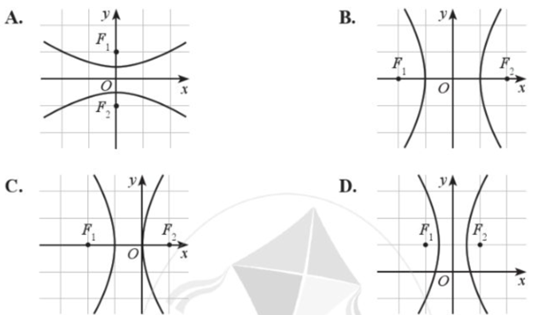
Hypebol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng:

\(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0)?

Phương trình nào sau đây là phương trình chính tắc của hypebol?

A. \({x^2} + \frac{{{y^2}}}{{{3^2}}} = 1\)              

B. \(\frac{{{x^2}}}{{16}} - {y^2} =  - 1\)          

C. \(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{9} =  - 1\)  

D. \({x^2} - \frac{{{y^2}}}{2} = 1\)

Phương trình nào sau đây là phương trình chính tắc của hypebol?

A. \({y^2} =  - 0,3x\)             

B. \({x^2} = 0,3y\)                 

C. \({y^2} = 0,3x\)                      

D. \({x^2} =  - 0,3y\)

Lập phương trình chính tắc của hypebol (H), biết (H) đi qua hai điểm M(-1 ; 0) và \(N(2;2\sqrt 3 )\).

Cho hypebol (H) có phương trình chính tắc: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) với a > 0, b > 0 và đường thẳng y = n cắt (H) tại hai điểm P, Q phân biệt. Chứng minh hai điểm P và Q đối xứng nhau qua trục Oy.

Phương trình nào dưới đây là phương trình chính tắc của đường hypebol?

A. \(\frac{{{x^2}}}{{{{15}^2}}} + \frac{{{y^2}}}{{{{15}^2}}} = 1\)           

B. \(\frac{{{x^2}}}{{{{15}^2}}} + \frac{{{y^2}}}{{{{16}^2}}} =  - 1\)

C. \(\frac{{{x^2}}}{{{{16}^2}}} + \frac{{{y^2}}}{{{{15}^2}}} = 1\)   

D. \(\frac{{{x^2}}}{{{{15}^2}}} - \frac{{{y^2}}}{{{{16}^2}}} = 1\)