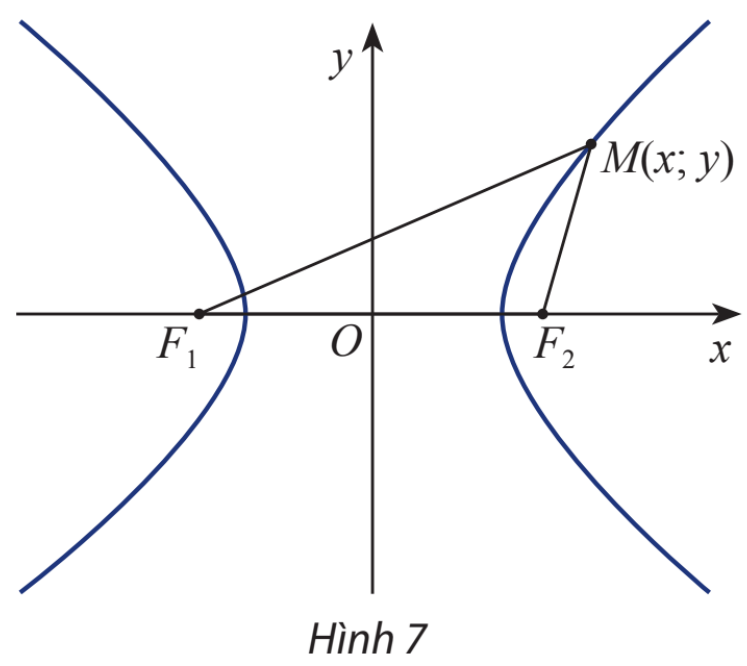
Cho hyperbol (H) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt điểm \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( - c;0)\) và \({F_2}(c;0)\).
Xét điểm \(M(x;y)\).
a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c.
b) Giải thích phát biểu sau:
\(M(x;y) \in (H) \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\).
Sử dụng phương pháp tọa độ trong mặt phẳng.
a) Ta có:
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x - c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \)
b) Ta có \(M(x;y) \in (E)\) nên \(\left| {{F_1}M - {F_2}M} \right| = 2a \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)
Các bài tập cùng chuyên đề
Cho (H): \(\frac{{{x^2}}}{{144}} - \frac{{{y^2}}}{{25}} = 1\). Tìm các tiêu điểm và tiêu cự của (H).
Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm của \({F_1}{F_2}\), tia Ox trùng tia\(O{F_2}\) , (H.7.26). Nêu toạ độ của các tiêu điềm \({F_1},{F_2}\). Giải thích vì sao điểm M(x; y) thuộc (H) khi và chỉ khi \(\left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\).
Cho hình chữ nhật ABCD và M, N tương ứng là trung điểm của các cạnh AB, CD (H725). Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N.
Tại sao trong định nghĩa hypebol cần điều kiện a < c?
Cho hyperbol có phương trình \(\frac{{{x^2}}}{7} - \frac{{{y^2}}}{9} = 1\). Tìm tiêu điểm và tiêu cự của hyperbol.
Phương trình nào sau đây là phương trình chính tắc của đường hyperbol?
A. \(\frac{{{x^2}}}{3} - \frac{{{y^2}}}{2} = - 1\)
B. \(\frac{{{x^2}}}{1} - \frac{{{y^2}}}{6} = 1\)
C. \(\frac{{{x^2}}}{6} + \frac{{{y^2}}}{1} = 1\)
D. \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{1} = - 1\)
Cho hypebol có phương trình: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
a) Tìm các giao điểm \({A_1},{A_2}\)của hypebol với trục hoành (hoành độ của \({A_1}\)nhỏ hơn của \({A_2}\)).
b) Chứng minh rằng, nếu điểm M(x; y) thuộc nhánh nằm bên trái trục tung của hypebol thì \(x \le - a\) , nêu điêm M(x, y) thuộc nhánh nằm bên phải trực tung của hypebol thì \(x \ge a\).
c) Tìm các điểm\({M_1},{M_2}\) tương ứng thuộc các nhánh bên trái, bên phải trực tung của hypebol để \({M_1}{M_2}\) nhỏ nhất.
Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục nhỏ bằng 6.
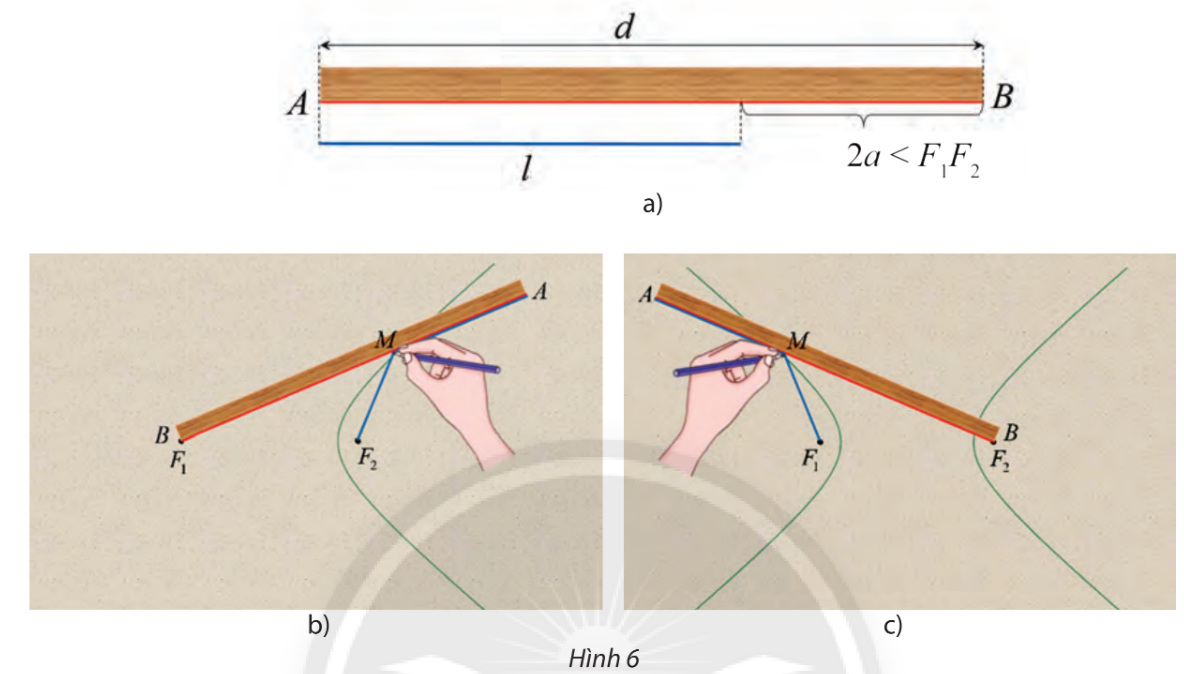
Lấy một tấm bìa, trên đó đánh dấu hai điểm \({F_1}\) và \({F_2}\). Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài l sao cho \(d - l = 2a\) nhỏ hơn khoảng cách \({F_1}{F_2}\) (hình 6a).
Đính một đầu dây vào đầu A của thước, dùng đinh ghim đầu dây còn lại vào điểm \({F_2}\). Đặt thước sao cho đầu B của thước trùng với điểm \({F_1}\). Tựa đầu bút chì vào dây, di chuyển điểm M trên tấm bìa và giữ sao cho dây luôn căng, đoạn AM ép sát vào thước, khi đó M sẽ gạch lên tấm bìa một đường (H) (xem hình 6b).
a) Chứng tỏ rằng khi M di động, ta luôn có \(M{F_1} - M{F_2} = 2a\).
b) Vẫn đính một đầu dây vào đầu A của thước nhưng đổi chỗ cố định đầu dây còn lại vào \({F_1}\), đầu B của thước trùng với \({F_2}\) sao cho đoạn thẳng BA có thể quay quanh \({F_2}\)và làm tương tự như lần đầu để bút chì M vẽ được một nhánh khác của đường (H) (hình 6c). Tính \(M{F_2} - M{F_1}\).
Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo của các hypebol sau:
a) \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
b) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
c) \({x^2} - 16{y^2} = 16\)
d) \(9{x^2} - 16{y^2} = 144\)
Viết phương trình chính tắc của hypebol thỏa mãn từng điều kiện sau:
a) Đỉnh \((3;0)\), tiêu điểm \((5;0)\)
b) Độ dài trục thực 8, độ dài trục ảo 6
Viết phương trình hypebol sau đây dưới dạng chính tắc: \(4{x^2}-9{y^2} = {\rm{ }}1.\)
Đóng hai chiếc đinh cố định tại hai điểm \({F_1},{F_2}\) trên mặt một bảng gỗ. Lấy một thước thẳng có mép AB và một sợi dây không đàn hồi có chiều dài \(l\) thoả mãn\(AB-{F_1}{F_2}{\rm{ }} < l < AB\) . Đính một đầu dây vào điểm A và đầu dây kia vào \({F_2}\). Đặt thước sao cho điểm B trùng với \({F_1}\), và lấy đầu bút chì (kí hiệu là M) tì sát sợi dây vào thước thẳng sao cho sợi dây luôn bị căng. Sợi dây khi đó là đường gấp khúc\(AM{F_2}\) , Cho thước quay quanh điểm B (trùng \({F_1}\)), tức là điểm A chuyển động trên đường tròn tâm B có bán kính bằng độ dài đoạn thẳng AB, mép thước luôn áp sát mặt gỗ (Hình 53). Khi đó, đầu bút chì M sẽ vạch nên một đường mà ta gọi là đường hypebol. Khi M thay đổi, có nhận xét gì về hiệu\(M{F_1} - M{F_2}\)?
Những phương trình nào sau đây là phương trình chính tắc của hypebol?
a) \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{9} = 1\)
b) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{9} = 1\)
c) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{64}} = 1\)
d) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{9} = 1\)
Tìm tọa độ các tiêu điểm của đường hypebol trong mỗi trường hợp sau:
a) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\)
b) \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{25}} = 1\)
Viết phương trình chính tắc của hypebol \(\left( H \right)\), biết \(N\left( {\sqrt {10} ;2} \right)\) nằm trên \(\left( H \right)\) và hoành độ một giao điểm của \(\left( H \right)\) với trục Ox bằng 3.
Cho hypebol \(\left( H \right)\) có phương trình \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{{20}} = 1\). Tìm tiêu điểm và tiêu cự của hypebol.
Viết phương trình chính tắc của hypebol \(\left( H \right)\), biết \(\left( H \right)\) đi qua điểm \(M\left( {3\sqrt 2 ; - 4} \right)\) và có một tiêu điểm \({F_2}\left( {5;0} \right)\).
Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường hypebol?
A. \(16{x^2} - 5{y^2} = - 80\)
B. \({x^2} = 4y\)
C. \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{1} = 1\)
D. \(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{1} = 1\)
Cho hypebol \(\left( H \right)\) có phương trình chính tắc \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{13}} = 1\). Tiêu cự của hypebol là:
A. 7
B. 14
C. \(2\sqrt {23} \)
D. \(\sqrt {23} \)
Phương trình chính tắc của hypebol có hai đỉnh \(\left( { - 4;0} \right),\left( {4;0} \right)\) và hai tiêu điểm là \(\left( { - 5;0} \right),\left( {5;0} \right)\) là:
A. \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{{25}} = 1\)
B. \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
C. \(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{9} = 1\)
D. \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\)
Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo các hypebol sau:
a) \(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{{144}} = 1\).
b) \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\).
Viết phương trình chính tắc của hypebol thỏa mãn các điều kiện sau:
a) Đỉnh \(\left( { - 6;0} \right)\) và \(\left( {6;0} \right)\); tiêu điểm \(\left( { - 10;0} \right)\) và \(\left( {10;0} \right)\).
b) Độ dài trục thực là 10, độ dài trục ảo là 20.
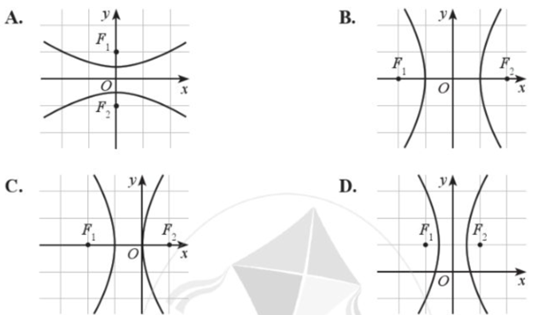
Hypebol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng:
\(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0)?
Phương trình nào sau đây là phương trình chính tắc của hypebol?
A. \({x^2} + \frac{{{y^2}}}{{{3^2}}} = 1\)
B. \(\frac{{{x^2}}}{{16}} - {y^2} = - 1\)
C. \(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{9} = - 1\)
D. \({x^2} - \frac{{{y^2}}}{2} = 1\)
Phương trình nào sau đây là phương trình chính tắc của hypebol?
A. \({y^2} = - 0,3x\)
B. \({x^2} = 0,3y\)
C. \({y^2} = 0,3x\)
D. \({x^2} = - 0,3y\)
Lập phương trình chính tắc của hypebol (H), biết (H) đi qua hai điểm M(-1 ; 0) và \(N(2;2\sqrt 3 )\).
Cho hypebol (H) có phương trình chính tắc: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) với a > 0, b > 0 và đường thẳng y = n cắt (H) tại hai điểm P, Q phân biệt. Chứng minh hai điểm P và Q đối xứng nhau qua trục Oy.
Phương trình nào dưới đây là phương trình chính tắc của đường hypebol?
A. \(\frac{{{x^2}}}{{{{15}^2}}} + \frac{{{y^2}}}{{{{15}^2}}} = 1\)
B. \(\frac{{{x^2}}}{{{{15}^2}}} + \frac{{{y^2}}}{{{{16}^2}}} = - 1\)
C. \(\frac{{{x^2}}}{{{{16}^2}}} + \frac{{{y^2}}}{{{{15}^2}}} = 1\)
D. \(\frac{{{x^2}}}{{{{15}^2}}} - \frac{{{y^2}}}{{{{16}^2}}} = 1\)
