Dân số nước Mỹ từ năm 1980 tới năm 1996 được tính theo công thức:
\(P = - 0,8{t^4} + 27{t^3} - 262{t^2} + 3010t + 227000\)
Và số người từ 85 tuổi trở lên thì tính theo công thức:
\(S = 0,02{t^4} - 0,7{t^3} + 6,4{t^2} + 213t + 7740\)
Trong đó P, S tính theo đơn vị nghìn người, t là số năm tính từ 1980. Viết biểu thức biểu thị số người Mỹ dưới 85 tuổi và tính số người đó vào năm 1995 (ứng với \(t = 15\)).
Thực hiện phép trừ đa thức một biến
Bước 1: Sắp xếp các đơn thức của hai đa thức cùng theo thứ tự lũy thừa giảm dần (hoặc tăng dần) của biến.
Bước 2: Thực hiện phép tính theo hàng ngang hoặc cột dọc.
Biểu thức biểu thị số người Mỹ dưới 85 tuổi là
\(\begin{array}{l}P - S = - 0,8{t^4} + 27{t^3} - 262{t^2} + 3010t + 227000 - \left( {0,02{t^4} - 0,7{t^3} + 6,4{t^2} + 213t + 7740} \right)\\ = - 0,82{t^4} + 27,7{t^3} - 268,4{t^2} + 2797t + 219260\end{array}\)
Khi \(t = 15\) thì số người Mỹ dưới 85 tuổi là
\(P - S = - 0,{82.15^4} + 27,{7.15^3} - 268,{4.15^2} + 2797.15 + 219260 = 252800\) người.
Các bài tập cùng chuyên đề
Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1
Tìm hiệu P – Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.
Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1
Tìm hiệu P – Q bằng cách đặt tính trừ: đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau rồi trừ theo từng cột.
Cho hai đa thức:
M = 0,5x4 – 4x3 + 2x – 2,5 và N = 2x3 + x2 + 1,5
Hãy tính hiệu M - N ( trình bày theo 2 cách)
Tìm hiệu sau theo cách đặt tính trừ: (- x3 – 5x + 2) – (3x + 8)
Một xe khách đi từ Hà Nội lên Yên Bái ( trên đường cao tốc Hà Nội – Lào Cai) với vận tốc 60 km/h. Sau đó 25 phút, một xe du lịch cũng đi từ Hà Nội lên Yên Bái ( đi cùng đường với xe khách) với vận tốc 85 km/h. Cả hai xe đều không nghỉ dọc đường.
a) Gọi D(x) là đa thức biểu thị quãng đường xe du lịch đi được và K(x) là đa thức biểu thị quãng đường xe khách đi được kể từ khi xuất phát cho đến khi xe du lịch đi được x giờ. Tìm D(x) và K(x).
b) Chứng tỏ rằng đa thức f(x) = K(x) – D(x) có nghiệm là x = 1. Hãy giải thích ý nghĩa nghiệm x = 1 của đa thức f(x).
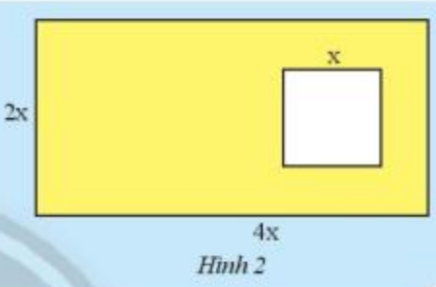
Hình 2 gồm một hình chữ nhật có chiều dài 4x cm, chiều rộng 2x cm và hình vuông nhỏ bên trong có cạnh x cm. Hãy lập biểu thức biểu thị diện tích của phần được tô màu vàng trong Hình 2.
Cho hai đa thức P(x) = \(2{x^3} - 9{x^2} + 5\) và Q(x) = \(2{x^2} + 4{x^3} - 7x\). Hãy tính P(x) – Q(x) bằng hai cách.
Cho tam giác (xem Hình 4) có chu vi bằng 12t – 3. Tìm cạnh chưa biết của tam giác đó.
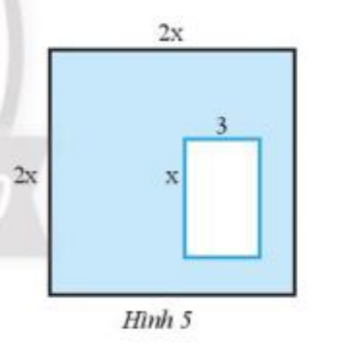
Cho hình vuông cạnh 2x và bên trong là hình chữ nhật có độ dài hai cạnh là x và 3 (Hình 5). Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh
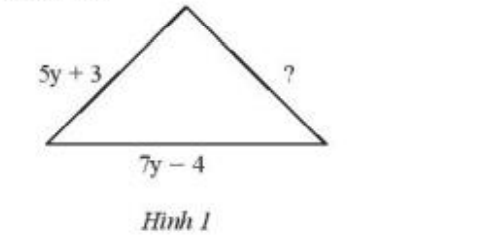
Tam giác trong Hình 1 có chu vi bằng (25y – 8) cm. Tìm cạnh chưa biết trong tam giác đó.
a) Thực hiện phép trừ trong mỗi trường hợp sau: \(2{x^2} - 6{x^2}\); \(a{x^k} - b{x^k}\)(k \(\in\) N*).
b) Nêu quy tắc trừ hai đơn thức có cùng số mũ của biến.
Cho hai đa thức:
\(P(x) = 4{x^2} + 1 + 3x\) và \(Q(x) = 5x + 2{x^2} + 3\).
a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến.
b) Tìm đơn thức thích hợp trong dạng thu gọn của P(x) và Q(x) cho ? ở bảng sau rồi trừ hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
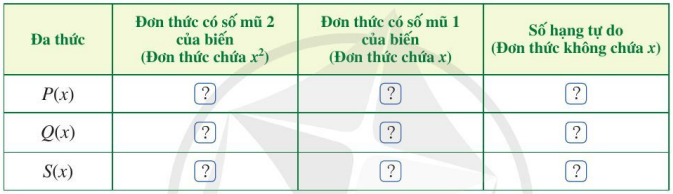
c) Dựa vào kết quả trừ hai đơn thức theo từng cột, xác định đơn thức S(x).
Cho hai đa thức:
\(P(x) = 2{x^2} - 5x - \dfrac{1}{3}\)
và \(Q(x) = - 6{x^4} + 5{x^2} + \dfrac{2}{3} + 3x\).
Tính hiệu P(x) – Q(x).
Cho hai đa thức:
\(P(x) = - 3{x^2} + 2 + 7x\) và \(Q(x) = - 4x + 5{x^2} + 1\).
a) Sắp xếp các đa thức P(x) và Q(x) theo số mũ giảm dần của biến.
b) Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc.
c) Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau.
d) Tính hiệu P(x) – Q(x) bằng cách thực hiện phép tính trong từng nhóm.
Tính hiệu P(x) – Q(x) bằng hai cách, trong đó:
\(\begin{array}{l}P(x) = 6{x^3} + 8{x^2} + 5x - 2;\\Q(x) = - 9{x^3} + 6{x^2} + 3 + 2x.\end{array}\)
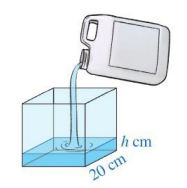
Người ta rót nước từ một can đựng 10 lít sang một bể rỗng có dạng hình lập phương với độ dài cạnh 20cm. Khi mực nước trong bể cao h (cm) thì thể tích nước trong can còn lại là bao nhiêu? Biết rằng 1 lít = 1\(d{m^3}\).
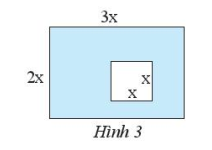
Hãy viết biểu thức biểu thị diện tích của phần tô đậm trong Hình 3.
Tam giác có độ dài hai cạnh là \(3y + 2\); \(6y - 4\) và chu vi bằng \(23y - 5\). Tìm cạnh chưa biết trong tam giác đó.
Cho đa thức \(F(x) = {x^7} - \frac{1}{2}{x^3} + x + 1\)
a) Tìm đa thức Q(x) sao cho F(x) + Q(x) = \({x^5} - {x^3} + 2\)
b) Tim đa thức R(x) sao cho F(x) – R(x) = 2
Tìm hiệu sau bằng cách đặt tính trừ: \(\left( { - {x^3} - 5x + 2} \right) - \left( {3x + 8} \right)\).
Trên một mảnh đất hình chữ nhật có chiều dài 65m, người ta định làm một bể bơi có chiều rộng là x mét, chiều dài gấp 3 lần chiều rộng. Sơ đồ và kích thước cụ thể (tính bằng mét) được cho trong hình bên.
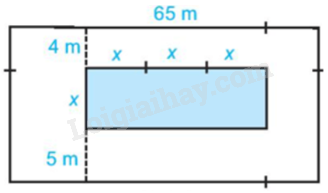
Tìm đa thức (biến x):
a) Biểu thị diện tích của bể bơi.
b) Biểu thị diện tích mảnh đất.
c) Biểu thị diện tích phần đất xung quanh bể bơi.
